Zyphra shares its research into a novel attention variant: Compressed Convolutional Attention (CCA). CCA dramatically reduces the compute, memory, and parameter costs of self-attention while matching or exceeding the performance of existing methods. Details of CCA and its grouped-query variant CCGQA are described in the accompanying technical report published to arXiv. CCGQA has been subsequently used to train the ZAYA suite of language models.
Self-attention is the powerful sequence mixer at the core of modern transformer architectures, but its quadratic compute complexity and linearly-growing KV-cache create fundamental bottlenecks for training and serving large language models—especially at long context lengths. Prior works such as Grouped Query Attention (GQA) and Multi-Latent Attention (MLA) have made important strides in reducing the KV-cache size and reducing decode latency. However, these methods leave FLOPs—which determines prefill and training speed—either unchanged or even increased.
We introduce Compressed Convolutional Attention (CCA), a novel attention method which down-projects queries, keys, and values to lower-dimensional latent space and then, crucially, performs the entire attention operation inside the shared latent space, unlike other attention mechanisms such as GQA and MLA. Our design cuts parameters, KV-cache, and FLOPs all at once by the desired compression factor. Since CCA is orthogonal to head-sharing approaches, we can combine the two to form Compressed Convolutional Grouped Query Attention (CCGQA), which enables the model designer to tune compression toward either FLOP or memory limits without sacrificing model quality. CCGQA is used to power the ZAYA suite of language models.

CCA builds on the insight that significant redundancy exists in traditional attention's parameter and activation spaces. Rather than up-projecting compressed representations back to full dimension before attention (as in MLA), CCA performs the full attention computation entirely within the compressed latent space.
To maintain and enhance performance at high compression rates, CCA introduces three key innovations:
Convolutional Mixing: We apply sequential convolutions across both sequence and channel dimensions on the compressed query and key latents. These convolutions provide additional expressivity and enable better information transfer through attention—analogous to how causal convolutions improve sequence mixing in state-space models.
QK-Mean Adaptation: We add the mean of pre- and post-convolution query and key values, which shares information between Q and K while providing a skip connection that allows the model to interpolate convolution strength.
Value-Shift: Each attention head receives two distinct value types—one from the current embedding and one from the previous position in the sequence. This inductive bias, similar to token-shift approaches in RWKV, proves beneficial for sequence modeling.
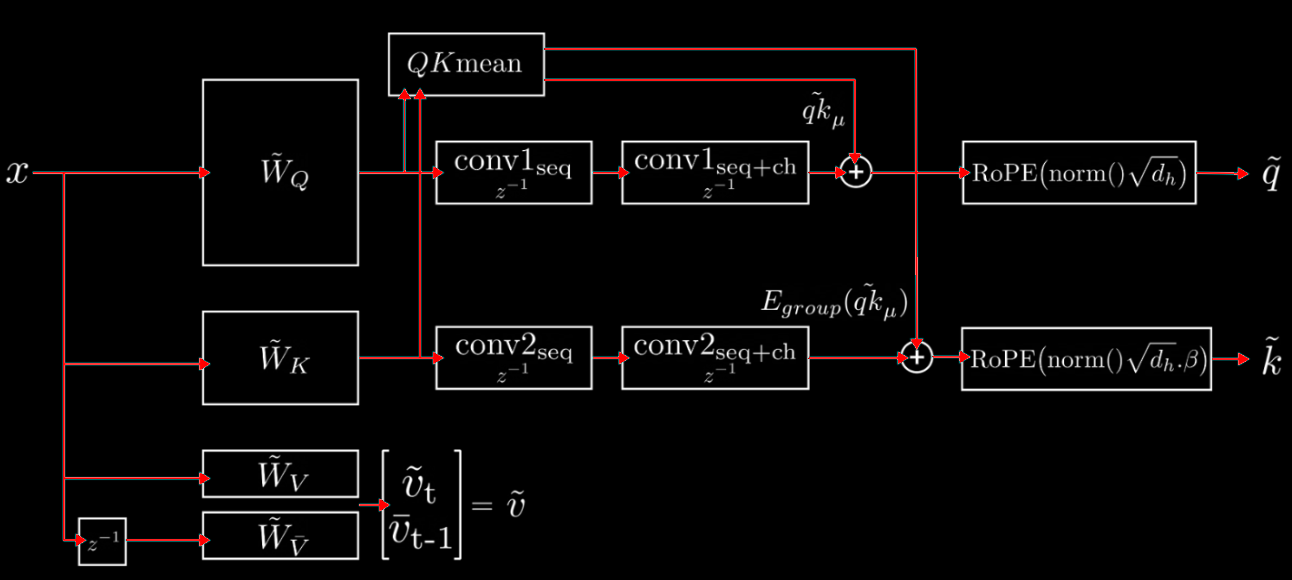
CCA allows RoPE (or any position embedding) to be applied directly within the latent space. This is unlike competing latent methods like MLA, which requires a shared key rope head and cache due to its up-projections.
Furthermore, our work is the first to note and theoretically clarify that parameter-sharing methods (like GQA) and parameter-compression methods (like MLA and CCA) are orthogonal and can be effectively combined. CCGQA applies GQA-style K and V head sharing within the already compressed latent space. This enables an additional 2× KV-cache reduction without performance penalty, and allows decoupling the compression rates of queries and keys.
In addition, CCA and CCGQA are also amenable to existing parallelism schemes:
Tensor Parallelism: Sharding CCA's latent representation incurs only the same cost as GQA, as long as TP rank matches the number of kv heads. The TP communication for QK mean can be overlapped with the compute of the convolutions.
Context Parallelism: One can communicate the smaller latent width E/C instead of full width E within ring or tree attention schemes.
Self-attention is the powerful sequence mixer at the core of modern transformer architectures, but its quadratic compute complexity and linearly-growing KV-cache create fundamental bottlenecks for training and serving large language models—especially at long context lengths. Prior works such as Grouped Query Attention (GQA) and Multi-Latent Attention (MLA) have made important strides in reducing the KV-cache size and reducing decode latency. However, these methods leave FLOPs—which determines prefill and training speed—either unchanged or even increased.
We introduce Compressed Convolutional Attention (CCA), a novel attention method which down-projects queries, keys, and values to lower-dimensional latent space and then, crucially, performs the entire attention operation inside the shared latent space, unlike other attention mechanisms such as GQA and MLA. Our design cuts parameters, KV-cache, and FLOPs all at once by the desired compression factor. Since CCA is orthogonal to head-sharing approaches, we can combine the two to form Compressed Convolutional Grouped Query Attention (CCGQA), which enables the model designer to tune compression toward either FLOP or memory limits without sacrificing model quality. CCGQA is used to power the ZAYA suite of language models.

CCA builds on the insight that significant redundancy exists in traditional attention's parameter and activation spaces. Rather than up-projecting compressed representations back to full dimension before attention (as in MLA), CCA performs the full attention computation entirely within the compressed latent space.
To maintain and enhance performance at high compression rates, CCA introduces three key innovations:
Convolutional Mixing: We apply sequential convolutions across both sequence and channel dimensions on the compressed query and key latents. These convolutions provide additional expressivity and enable better information transfer through attention—analogous to how causal convolutions improve sequence mixing in state-space models.
QK-Mean Adaptation: We add the mean of pre- and post-convolution query and key values, which shares information between Q and K while providing a skip connection that allows the model to interpolate convolution strength.
Value-Shift: Each attention head receives two distinct value types—one from the current embedding and one from the previous position in the sequence. This inductive bias, similar to token-shift approaches in RWKV, proves beneficial for sequence modeling.

CCA allows RoPE (or any position embedding) to be applied directly within the latent space. This is unlike competing latent methods like MLA, which requires a shared key rope head and cache due to its up-projections.
Furthermore, our work is the first to note and theoretically clarify that parameter-sharing methods (like GQA) and parameter-compression methods (like MLA and CCA) are orthogonal and can be effectively combined. CCGQA applies GQA-style K and V head sharing within the already compressed latent space. This enables an additional 2× KV-cache reduction without performance penalty, and allows decoupling the compression rates of queries and keys.
In addition, CCA and CCGQA are also amenable to existing parallelism schemes:
Tensor Parallelism: Sharding CCA's latent representation incurs only the same cost as GQA, as long as TP rank matches the number of kv heads. The TP communication for QK mean can be overlapped with the compute of the convolutions.
Context Parallelism: One can communicate the smaller latent width E/C instead of full width E within ring or tree attention schemes.
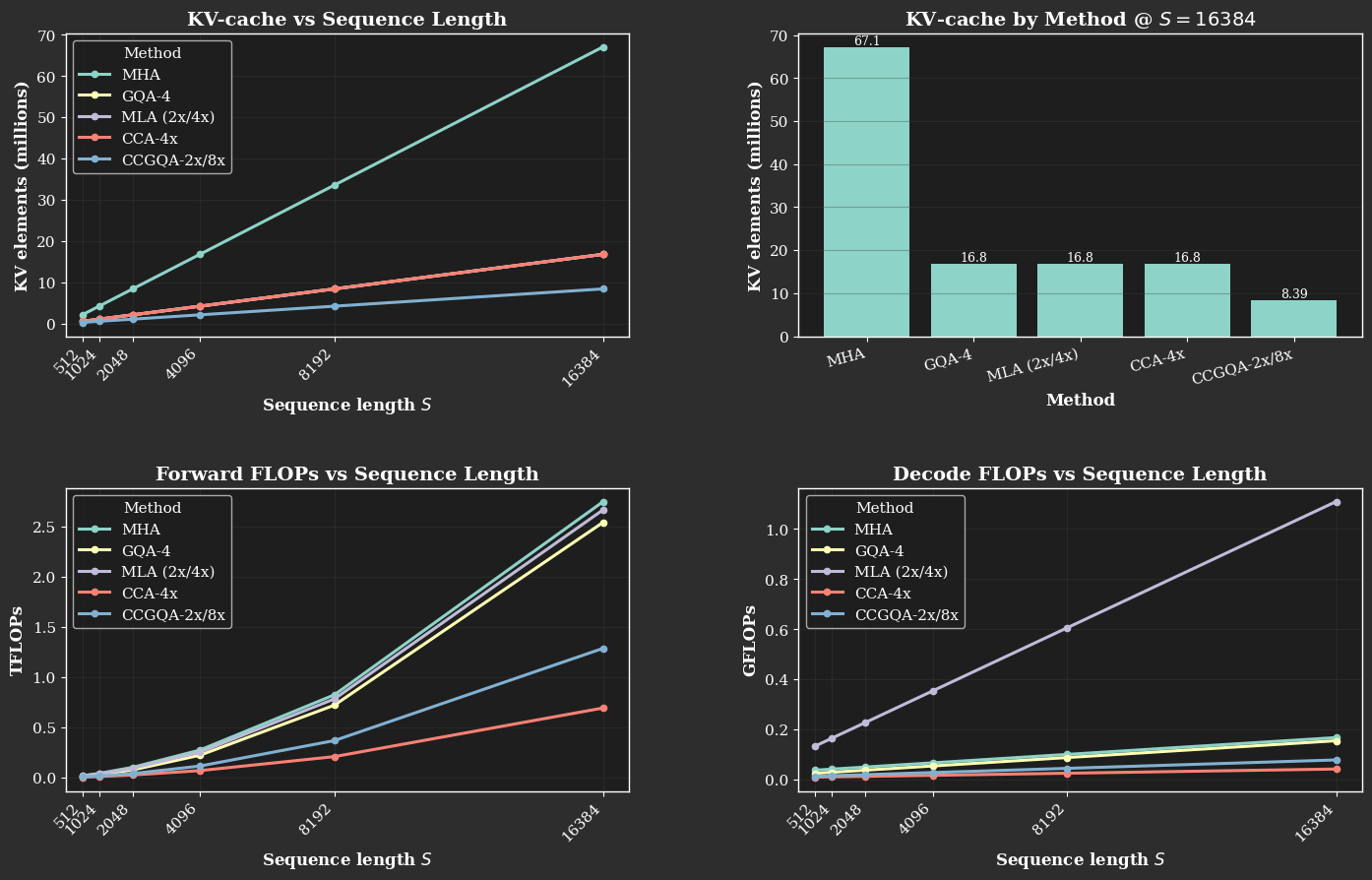
Because the S² terms in QKᵀ and Attn·V shrink by 1/C (where C is the compression factor), the speedups grow with sequence length. On H100 GPUs, our fused CCA kernel reduces prefill latency by approximately 1.7× at sequence length 16k relative to MHA, and accelerates backward passes by approximately 1.3×.
CCA with 16× compression enables √16 = 4× longer sequences to be processed for the same FLOP budget. For a full theoretical FLOP analysis of CCA against its competitors, see Table II and Figure 2 (below) of the technical report.
Because the S² terms in QKᵀ and Attn·V shrink by 1/C (where C is the compression factor), the speedups grow with sequence length. On H100 GPUs, our fused CCA kernel reduces prefill latency by approximately 1.7× at sequence length 16k relative to MHA, and accelerates backward passes by approximately 1.3×.
CCA with 16× compression enables √16 = 4× longer sequences to be processed for the same FLOP budget. For a full theoretical FLOP analysis of CCA against its competitors, see Table II and Figure 2 (below) of the technical report.
Self-attention is the powerful sequence mixer at the core of modern transformer architectures, but its quadratic compute complexity and linearly-growing KV-cache create fundamental bottlenecks for training and serving large language models—especially at long context lengths. Prior works such as Grouped Query Attention (GQA) and Multi-Latent Attention (MLA) have made important strides in reducing the KV-cache size and reducing decode latency. However, these methods leave FLOPs—which determines prefill and training speed—either unchanged or even increased.
We introduce Compressed Convolutional Attention (CCA), a novel attention method which down-projects queries, keys, and values to lower-dimensional latent space and then, crucially, performs the entire attention operation inside the shared latent space, unlike other attention mechanisms such as GQA and MLA. Our design cuts parameters, KV-cache, and FLOPs all at once by the desired compression factor. Since CCA is orthogonal to head-sharing approaches, we can combine the two to form Compressed Convolutional Grouped Query Attention (CCGQA), which enables the model designer to tune compression toward either FLOP or memory limits without sacrificing model quality. CCGQA is used to power the ZAYA suite of language models.

Because the S² terms in QKᵀ and Attn·V shrink by 1/C (where C is the compression factor), the speedups grow with sequence length. On H100 GPUs, our fused CCA kernel reduces prefill latency by approximately 1.7× at sequence length 16k relative to MHA, and accelerates backward passes by approximately 1.3×.
CCA with 16× compression enables √16 = 4× longer sequences to be processed for the same FLOP budget. For a full theoretical FLOP analysis of CCA against its competitors, see Table II and Figure 2 (below) of the technical report.
CCA builds on the insight that significant redundancy exists in traditional attention's parameter and activation spaces. Rather than up-projecting compressed representations back to full dimension before attention (as in MLA), CCA performs the full attention computation entirely within the compressed latent space.
To maintain and enhance performance at high compression rates, CCA introduces three key innovations:
Convolutional Mixing: We apply sequential convolutions across both sequence and channel dimensions on the compressed query and key latents. These convolutions provide additional expressivity and enable better information transfer through attention—analogous to how causal convolutions improve sequence mixing in state-space models.
QK-Mean Adaptation: We add the mean of pre- and post-convolution query and key values, which shares information between Q and K while providing a skip connection that allows the model to interpolate convolution strength.
Value-Shift: Each attention head receives two distinct value types—one from the current embedding and one from the previous position in the sequence. This inductive bias, similar to token-shift approaches in RWKV, proves beneficial for sequence modeling.

Because the S² terms in QKᵀ and Attn·V shrink by 1/C (where C is the compression factor), the speedups grow with sequence length. On H100 GPUs, our fused CCA kernel reduces prefill latency by approximately 1.7× at sequence length 16k relative to MHA, and accelerates backward passes by approximately 1.3×.
CCA with 16× compression enables √16 = 4× longer sequences to be processed for the same FLOP budget. For a full theoretical FLOP analysis of CCA against its competitors, see Table II and Figure 2 (below) of the technical report.

Because the S² terms in QKᵀ and Attn·V shrink by 1/C (where C is the compression factor), the speedups grow with sequence length. On H100 GPUs, our fused CCA kernel reduces prefill latency by approximately 1.7× at sequence length 16k relative to MHA, and accelerates backward passes by approximately 1.3×.
CCA with 16× compression enables √16 = 4× longer sequences to be processed for the same FLOP budget. For a full theoretical FLOP analysis of CCA against its competitors, see Table II and Figure 2 (below) of the technical report.
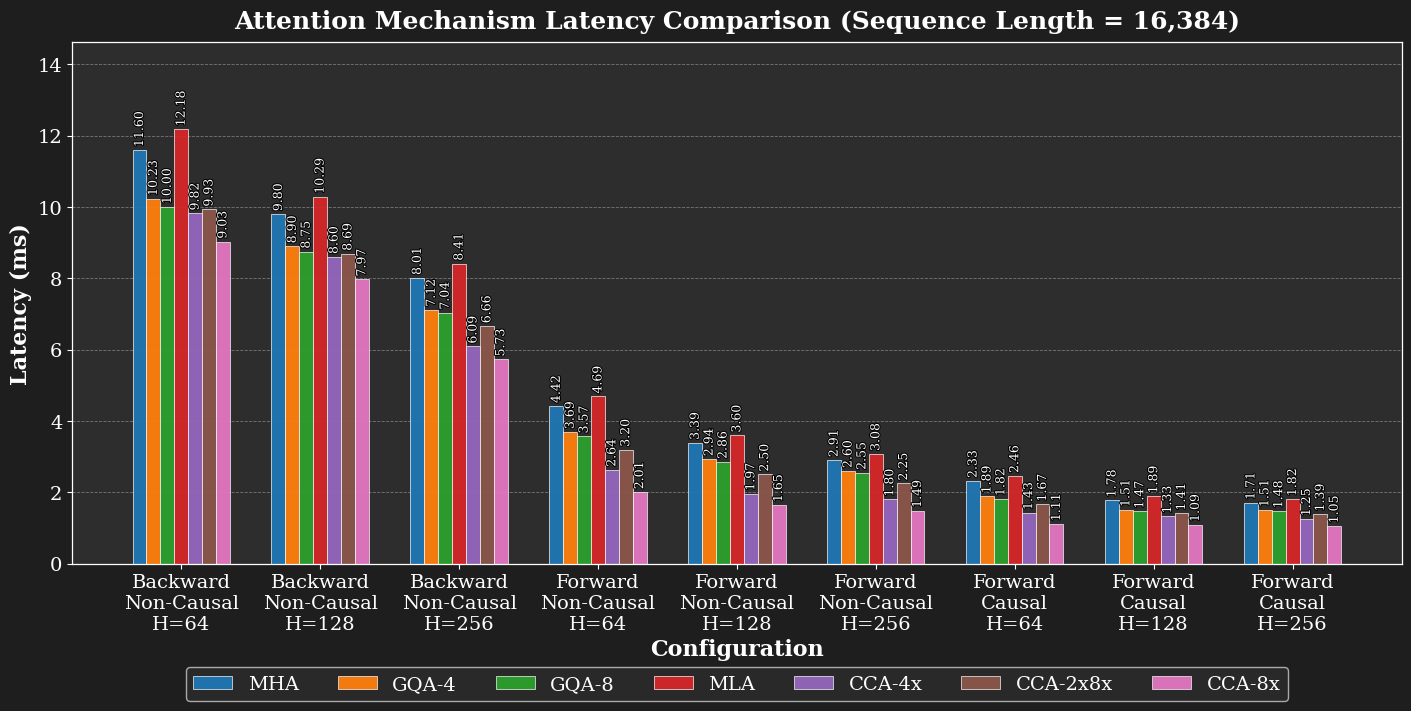
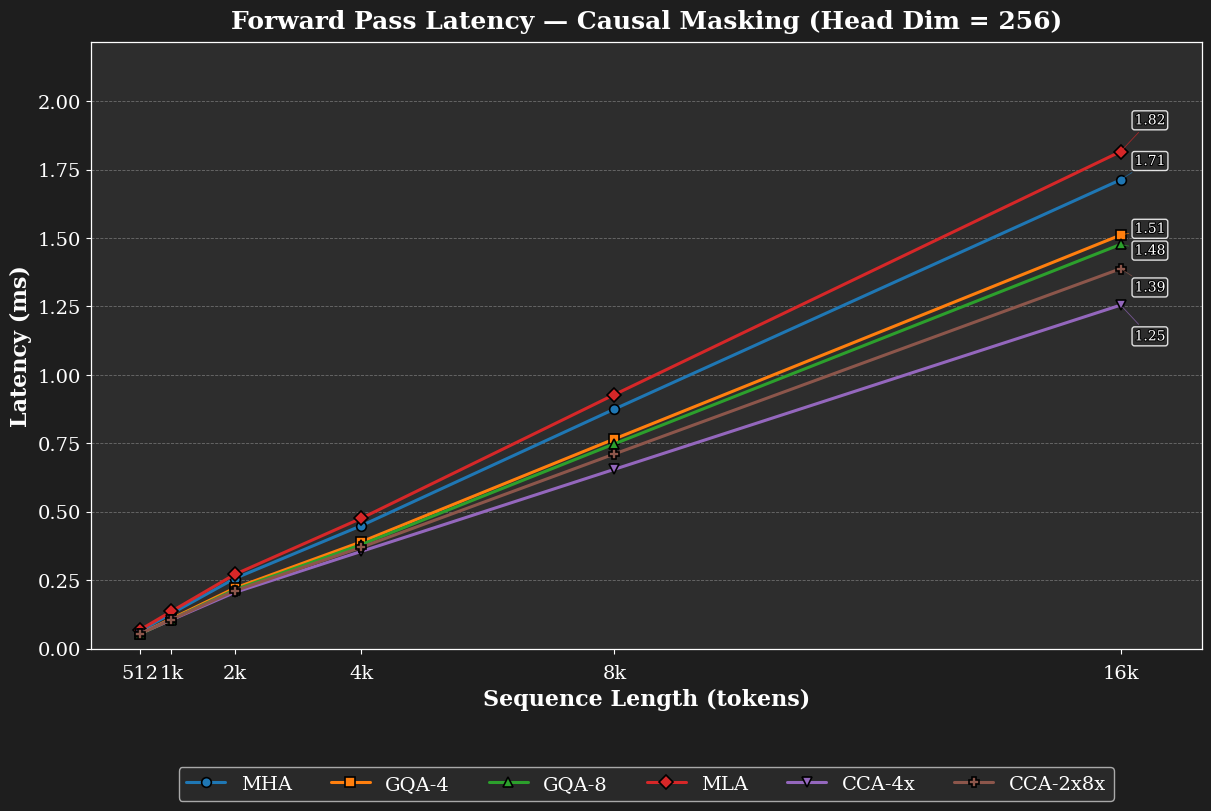
Because the S² terms in QKᵀ and Attn·V shrink by 1/C (where C is the compression factor), the speedups grow with sequence length. On H100 GPUs, our fused CCA kernel reduces prefill latency by approximately 1.7× at sequence length 16k relative to MHA, and accelerates backward passes by approximately 1.3×.
CCA with 16× compression enables √16 = 4× longer sequences to be processed for the same FLOP budget. For a full theoretical FLOP analysis of CCA against its competitors, see Table II and Figure 2 (below) of the technical report.
To realize these theoretical gains in practice, we designed and implemented H100 GPU kernels for the forward and backward that fuses the convolution operations with an online softmax in the style of Flash Attention. The kernel executes the entire attention operation in the compressed latent space of width E/C, which significantly reduces both the arithmetic intensity and data-movement requirements.
Our FLOP complexity model closely aligns with implementation results. The matrix multiplications of CCA reduce by a factor of 1/C. CCA’s lead grows with larger sequence lengths as the S² terms and projections dominate and the small overheads from convolutions, reductions, and kernel launch amortize. A key difference from methods that only rebalance bandwidth during decode (like GQA and MLA) is that CCA reduces both prefill and decode compute while simultaneously shrinking the KV-cache. CCGQA inherits GQA's KV reuse benefits in the latent while preserving CCA's 1/C scaling of the matrix multiplications. This enables CCA to provide significant performance benefits during training, prefill, and decode.
Self-attention is the powerful sequence mixer at the core of modern transformer architectures, but its quadratic compute complexity and linearly-growing KV-cache create fundamental bottlenecks for training and serving large language models—especially at long context lengths. Prior works such as Grouped Query Attention (GQA) and Multi-Latent Attention (MLA) have made important strides in reducing the KV-cache size and reducing decode latency. However, these methods leave FLOPs—which determines prefill and training speed—either unchanged or even increased.
We introduce Compressed Convolutional Attention (CCA), a novel attention method which down-projects queries, keys, and values to lower-dimensional latent space and then, crucially, performs the entire attention operation inside the shared latent space, unlike other attention mechanisms such as GQA and MLA. Our design cuts parameters, KV-cache, and FLOPs all at once by the desired compression factor. Since CCA is orthogonal to head-sharing approaches, we can combine the two to form Compressed Convolutional Grouped Query Attention (CCGQA), which enables the model designer to tune compression toward either FLOP or memory limits without sacrificing model quality. CCGQA is used to power the ZAYA suite of language models.

CCA builds on the insight that significant redundancy exists in traditional attention's parameter and activation spaces. Rather than up-projecting compressed representations back to full dimension before attention (as in MLA), CCA performs the full attention computation entirely within the compressed latent space.
To maintain and enhance performance at high compression rates, CCA introduces three key innovations:
Convolutional Mixing: We apply sequential convolutions across both sequence and channel dimensions on the compressed query and key latents. These convolutions provide additional expressivity and enable better information transfer through attention—analogous to how causal convolutions improve sequence mixing in state-space models.
QK-Mean Adaptation: We add the mean of pre- and post-convolution query and key values, which shares information between Q and K while providing a skip connection that allows the model to interpolate convolution strength.
Value-Shift: Each attention head receives two distinct value types—one from the current embedding and one from the previous position in the sequence. This inductive bias, similar to token-shift approaches in RWKV, proves beneficial for sequence modeling.
CCA allows RoPE (or any position embedding) to be applied directly within the latent space. This is unlike competing latent methods like MLA, which requires a shared key rope head and cache due to its up-projections.
Furthermore, our work is the first to note and theoretically clarify that parameter-sharing methods (like GQA) and parameter-compression methods (like MLA and CCA) are orthogonal and can be effectively combined. CCGQA applies GQA-style K and V head sharing within the already compressed latent space. This enables an additional 2× KV-cache reduction without performance penalty, and allows decoupling the compression rates of queries and keys.
In addition, CCA and CCGQA are also amenable to existing parallelism schemes:
Tensor Parallelism: Sharding CCA's latent representation incurs only the same cost as GQA, as long as TP rank matches the number of kv heads. The TP communication for QK mean can be overlapped with the compute of the convolutions.
Context Parallelism: One can communicate the smaller latent width E/C instead of full width E within ring or tree attention schemes.

Because the S² terms in QKᵀ and Attn·V shrink by 1/C (where C is the compression factor), the speedups grow with sequence length. On H100 GPUs, our fused CCA kernel reduces prefill latency by approximately 1.7× at sequence length 16k relative to MHA, and accelerates backward passes by approximately 1.3×.
CCA with 16× compression enables √16 = 4× longer sequences to be processed for the same FLOP budget. For a full theoretical FLOP analysis of CCA against its competitors, see Table II and Figure 2 (below) of the technical report.

To realize these theoretical gains in practice, we designed and implemented H100 GPU kernels for the forward and backward that fuses the convolution operations with an online softmax in the style of Flash Attention. The kernel executes the entire attention operation in the compressed latent space of width E/C, which significantly reduces both the arithmetic intensity and data-movement requirements.
Our FLOP complexity model closely aligns with implementation results. The matrix multiplications of CCA reduce by a factor of 1/C. CCA’s lead grows with larger sequence lengths as the S² terms and projections dominate and the small overheads from convolutions, reductions, and kernel launch amortize. A key difference from methods that only rebalance bandwidth during decode (like GQA and MLA) is that CCA reduces both prefill and decode compute while simultaneously shrinking the KV-cache. CCGQA inherits GQA's KV reuse benefits in the latent while preserving CCA's 1/C scaling of the matrix multiplications. This enables CCA to provide significant performance benefits during training, prefill, and decode.

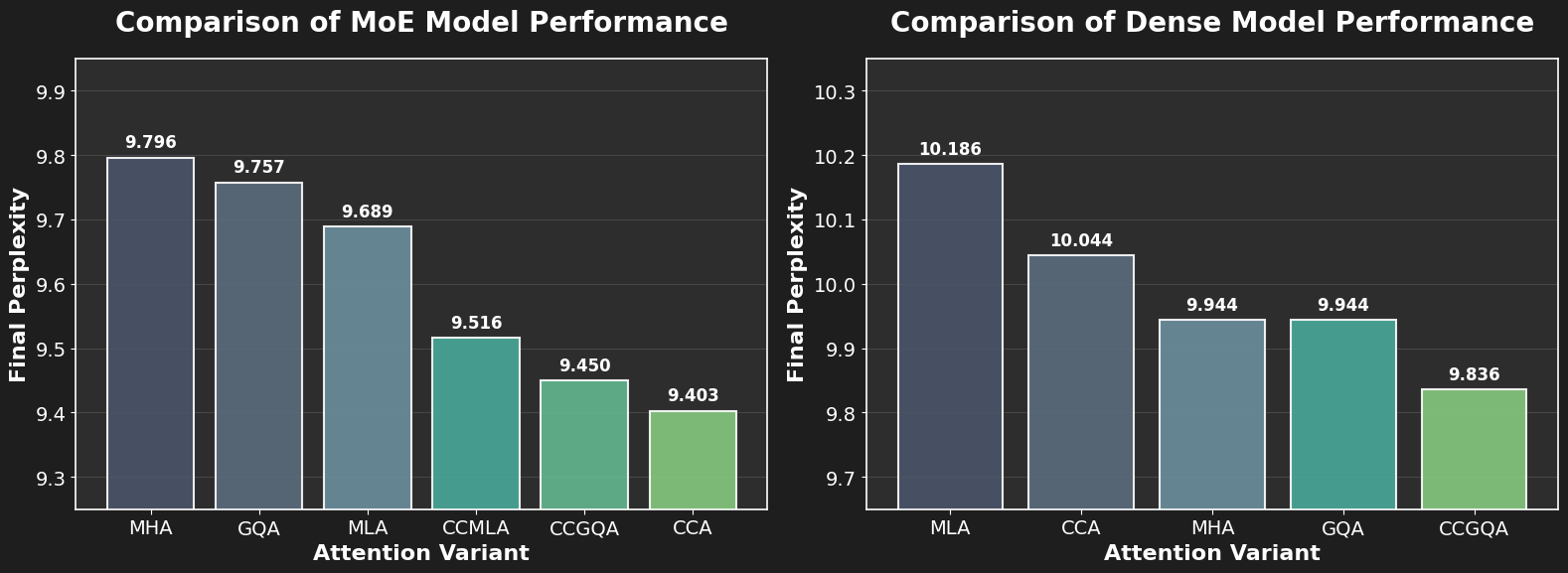
Our experimental ablations demonstrate that CCA and CCGQA consistently outperform both GQA and MLA at equal KV-cache compression on both dense and MoE models.
Dense Models: CCGQA outperforms all other attentions despite matching parameters—with substantial KV-cache compression compared to MHA. CCA beats MLA in the parameter-matched setting while using 4 times fewer FLOPs.
MoE Models: CCA achieves lower loss than GQA and MLA at equivalent parameter counts with less compute cost. CCGQA achieves 8× KV-cache compression, half the KV-cache of other parameter efficient attentions tested, with no drop in performance compared to standard MHA and other parameter efficient attentions such as MLA.
The full technical report, including ablation studies, kernel implementation details, and code examples, is available on arXiv. For an example of using CCA/CCGQA in a production model training run, see our ZAYA1 technical report.
Self-attention is the powerful sequence mixer at the core of modern transformer architectures, but its quadratic compute complexity and linearly-growing KV-cache create fundamental bottlenecks for training and serving large language models—especially at long context lengths. Prior works such as Grouped Query Attention (GQA) and Multi-Latent Attention (MLA) have made important strides in reducing the KV-cache size and reducing decode latency. However, these methods leave FLOPs—which determines prefill and training speed—either unchanged or even increased.
We introduce Compressed Convolutional Attention (CCA), a novel attention method which down-projects queries, keys, and values to lower-dimensional latent space and then, crucially, performs the entire attention operation inside the shared latent space, unlike other attention mechanisms such as GQA and MLA. Our design cuts parameters, KV-cache, and FLOPs all at once by the desired compression factor. Since CCA is orthogonal to head-sharing approaches, we can combine the two to form Compressed Convolutional Grouped Query Attention (CCGQA), which enables the model designer to tune compression toward either FLOP or memory limits without sacrificing model quality. CCGQA is used to power the ZAYA suite of language models.
CCA builds on the insight that significant redundancy exists in traditional attention's parameter and activation spaces. Rather than up-projecting compressed representations back to full dimension before attention (as in MLA), CCA performs the full attention computation entirely within the compressed latent space.
To maintain and enhance performance at high compression rates, CCA introduces three key innovations:
Convolutional Mixing: We apply sequential convolutions across both sequence and channel dimensions on the compressed query and key latents. These convolutions provide additional expressivity and enable better information transfer through attention—analogous to how causal convolutions improve sequence mixing in state-space models.
QK-Mean Adaptation: We add the mean of pre- and post-convolution query and key values, which shares information between Q and K while providing a skip connection that allows the model to interpolate convolution strength.
Value-Shift: Each attention head receives two distinct value types—one from the current embedding and one from the previous position in the sequence. This inductive bias, similar to token-shift approaches in RWKV, proves beneficial for sequence modeling.

CCA allows RoPE (or any position embedding) to be applied directly within the latent space. This is unlike competing latent methods like MLA, which requires a shared key rope head and cache due to its up-projections.
Furthermore, our work is the first to note and theoretically clarify that parameter-sharing methods (like GQA) and parameter-compression methods (like MLA and CCA) are orthogonal and can be effectively combined. CCGQA applies GQA-style K and V head sharing within the already compressed latent space. This enables an additional 2× KV-cache reduction without performance penalty, and allows decoupling the compression rates of queries and keys.
In addition, CCA and CCGQA are also amenable to existing parallelism schemes:
Tensor Parallelism: Sharding CCA's latent representation incurs only the same cost as GQA, as long as TP rank matches the number of kv heads. The TP communication for QK mean can be overlapped with the compute of the convolutions.
Context Parallelism: One can communicate the smaller latent width E/C instead of full width E within ring or tree attention schemes.
Because the S² terms in QKᵀ and Attn·V shrink by 1/C (where C is the compression factor), the speedups grow with sequence length. On H100 GPUs, our fused CCA kernel reduces prefill latency by approximately 1.7× at sequence length 16k relative to MHA, and accelerates backward passes by approximately 1.3×.
CCA with 16× compression enables √16 = 4× longer sequences to be processed for the same FLOP budget. For a full theoretical FLOP analysis of CCA against its competitors, see Table II and Figure 2 (below) of the technical report.

To realize these theoretical gains in practice, we designed and implemented H100 GPU kernels for the forward and backward that fuses the convolution operations with an online softmax in the style of Flash Attention. The kernel executes the entire attention operation in the compressed latent space of width E/C, which significantly reduces both the arithmetic intensity and data-movement requirements.
Our FLOP complexity model closely aligns with implementation results. The matrix multiplications of CCA reduce by a factor of 1/C. CCA’s lead grows with larger sequence lengths as the S² terms and projections dominate and the small overheads from convolutions, reductions, and kernel launch amortize. A key difference from methods that only rebalance bandwidth during decode (like GQA and MLA) is that CCA reduces both prefill and decode compute while simultaneously shrinking the KV-cache. CCGQA inherits GQA's KV reuse benefits in the latent while preserving CCA's 1/C scaling of the matrix multiplications. This enables CCA to provide significant performance benefits during training, prefill, and decode.

Our experimental ablations demonstrate that CCA and CCGQA consistently outperform both GQA and MLA at equal KV-cache compression on both dense and MoE models.
Dense Models: CCGQA outperforms all other attentions despite matching parameters—with substantial KV-cache compression compared to MHA. CCA beats MLA in the parameter-matched setting while using 4 times fewer FLOPs.
MoE Models: CCA achieves lower loss than GQA and MLA at equivalent parameter counts with less compute cost. CCGQA achieves 8× KV-cache compression, half the KV-cache of other parameter efficient attentions tested, with no drop in performance compared to standard MHA and other parameter efficient attentions such as MLA.
The full technical report, including ablation studies, kernel implementation details, and code examples, is available on arXiv. For an example of using CCA/CCGQA in a production model training run, see our ZAYA1 technical report.
Self-attention is the powerful sequence mixer at the core of modern transformer architectures, but its quadratic compute complexity and linearly-growing KV-cache create fundamental bottlenecks for training and serving large language models—especially at long context lengths. Prior works such as Grouped Query Attention (GQA) and Multi-Latent Attention (MLA) have made important strides in reducing the KV-cache size and reducing decode latency. However, these methods leave FLOPs—which determines prefill and training speed—either unchanged or even increased.
We introduce Compressed Convolutional Attention (CCA), a novel attention method which down-projects queries, keys, and values to lower-dimensional latent space and then, crucially, performs the entire attention operation inside the shared latent space, unlike other attention mechanisms such as GQA and MLA. Our design cuts parameters, KV-cache, and FLOPs all at once by the desired compression factor. Since CCA is orthogonal to head-sharing approaches, we can combine the two to form Compressed Convolutional Grouped Query Attention (CCGQA), which enables the model designer to tune compression toward either FLOP or memory limits without sacrificing model quality. CCGQA is used to power the ZAYA suite of language models.
CCA builds on the insight that significant redundancy exists in traditional attention's parameter and activation spaces. Rather than up-projecting compressed representations back to full dimension before attention (as in MLA), CCA performs the full attention computation entirely within the compressed latent space.
To maintain and enhance performance at high compression rates, CCA introduces three key innovations:
Convolutional Mixing: We apply sequential convolutions across both sequence and channel dimensions on the compressed query and key latents. These convolutions provide additional expressivity and enable better information transfer through attention—analogous to how causal convolutions improve sequence mixing in state-space models.
QK-Mean Adaptation: We add the mean of pre- and post-convolution query and key values, which shares information between Q and K while providing a skip connection that allows the model to interpolate convolution strength.
Value-Shift: Each attention head receives two distinct value types—one from the current embedding and one from the previous position in the sequence. This inductive bias, similar to token-shift approaches in RWKV, proves beneficial for sequence modeling.

CCA allows RoPE (or any position embedding) to be applied directly within the latent space. This is unlike competing latent methods like MLA, which requires a shared key rope head and cache due to its up-projections.
Furthermore, our work is the first to note and theoretically clarify that parameter-sharing methods (like GQA) and parameter-compression methods (like MLA and CCA) are orthogonal and can be effectively combined. CCGQA applies GQA-style K and V head sharing within the already compressed latent space. This enables an additional 2× KV-cache reduction without performance penalty, and allows decoupling the compression rates of queries and keys.
In addition, CCA and CCGQA are also amenable to existing parallelism schemes:
Tensor Parallelism: Sharding CCA's latent representation incurs only the same cost as GQA, as long as TP rank matches the number of kv heads. The TP communication for QK mean can be overlapped with the compute of the convolutions.
Context Parallelism: One can communicate the smaller latent width E/C instead of full width E within ring or tree attention schemes.

Because the S² terms in QKᵀ and Attn·V shrink by 1/C (where C is the compression factor), the speedups grow with sequence length. On H100 GPUs, our fused CCA kernel reduces prefill latency by approximately 1.7× at sequence length 16k relative to MHA, and accelerates backward passes by approximately 1.3×.
CCA with 16× compression enables √16 = 4× longer sequences to be processed for the same FLOP budget. For a full theoretical FLOP analysis of CCA against its competitors, see Table II and Figure 2 (below) of the technical report.

To realize these theoretical gains in practice, we designed and implemented H100 GPU kernels for the forward and backward that fuses the convolution operations with an online softmax in the style of Flash Attention. The kernel executes the entire attention operation in the compressed latent space of width E/C, which significantly reduces both the arithmetic intensity and data-movement requirements.
Our FLOP complexity model closely aligns with implementation results. The matrix multiplications of CCA reduce by a factor of 1/C. CCA’s lead grows with larger sequence lengths as the S² terms and projections dominate and the small overheads from convolutions, reductions, and kernel launch amortize. A key difference from methods that only rebalance bandwidth during decode (like GQA and MLA) is that CCA reduces both prefill and decode compute while simultaneously shrinking the KV-cache. CCGQA inherits GQA's KV reuse benefits in the latent while preserving CCA's 1/C scaling of the matrix multiplications. This enables CCA to provide significant performance benefits during training, prefill, and decode.
Our experimental ablations demonstrate that CCA and CCGQA consistently outperform both GQA and MLA at equal KV-cache compression on both dense and MoE models.
Dense Models: CCGQA outperforms all other attentions despite matching parameters—with substantial KV-cache compression compared to MHA. CCA beats MLA in the parameter-matched setting while using 4 times fewer FLOPs.
MoE Models: CCA achieves lower loss than GQA and MLA at equivalent parameter counts with less compute cost. CCGQA achieves 8× KV-cache compression, half the KV-cache of other parameter efficient attentions tested, with no drop in performance compared to standard MHA and other parameter efficient attentions such as MLA.
Self-attention is the powerful sequence mixer at the core of modern transformer architectures, but its quadratic compute complexity and linearly-growing KV-cache create fundamental bottlenecks for training and serving large language models—especially at long context lengths. Prior works such as Grouped Query Attention (GQA) and Multi-Latent Attention (MLA) have made important strides in reducing the KV-cache size and reducing decode latency. However, these methods leave FLOPs—which determines prefill and training speed—either unchanged or even increased.
We introduce Compressed Convolutional Attention (CCA), a novel attention method which down-projects queries, keys, and values to lower-dimensional latent space and then, crucially, performs the entire attention operation inside the shared latent space, unlike other attention mechanisms such as GQA and MLA. Our design cuts parameters, KV-cache, and FLOPs all at once by the desired compression factor. Since CCA is orthogonal to head-sharing approaches, we can combine the two to form Compressed Convolutional Grouped Query Attention (CCGQA), which enables the model designer to tune compression toward either FLOP or memory limits without sacrificing model quality. CCGQA is used to power the ZAYA suite of language models.

CCA builds on the insight that significant redundancy exists in traditional attention's parameter and activation spaces. Rather than up-projecting compressed representations back to full dimension before attention (as in MLA), CCA performs the full attention computation entirely within the compressed latent space.
To maintain and enhance performance at high compression rates, CCA introduces three key innovations:
Convolutional Mixing: We apply sequential convolutions across both sequence and channel dimensions on the compressed query and key latents. These convolutions provide additional expressivity and enable better information transfer through attention—analogous to how causal convolutions improve sequence mixing in state-space models.
QK-Mean Adaptation: We add the mean of pre- and post-convolution query and key values, which shares information between Q and K while providing a skip connection that allows the model to interpolate convolution strength.
Value-Shift: Each attention head receives two distinct value types—one from the current embedding and one from the previous position in the sequence. This inductive bias, similar to token-shift approaches in RWKV, proves beneficial for sequence modeling.
CCA allows RoPE (or any position embedding) to be applied directly within the latent space. This is unlike competing latent methods like MLA, which requires a shared key rope head and cache due to its up-projections.
Furthermore, our work is the first to note and theoretically clarify that parameter-sharing methods (like GQA) and parameter-compression methods (like MLA and CCA) are orthogonal and can be effectively combined. CCGQA applies GQA-style K and V head sharing within the already compressed latent space. This enables an additional 2× KV-cache reduction without performance penalty, and allows decoupling the compression rates of queries and keys.
In addition, CCA and CCGQA are also amenable to existing parallelism schemes:
Tensor Parallelism: Sharding CCA's latent representation incurs only the same cost as GQA, as long as TP rank matches the number of kv heads. The TP communication for QK mean can be overlapped with the compute of the convolutions.
Context Parallelism: One can communicate the smaller latent width E/C instead of full width E within ring or tree attention schemes.
Because the S² terms in QKᵀ and Attn·V shrink by 1/C (where C is the compression factor), the speedups grow with sequence length. On H100 GPUs, our fused CCA kernel reduces prefill latency by approximately 1.7× at sequence length 16k relative to MHA, and accelerates backward passes by approximately 1.3×.
CCA with 16× compression enables √16 = 4× longer sequences to be processed for the same FLOP budget. For a full theoretical FLOP analysis of CCA against its competitors, see Table II and Figure 2 (below) of the technical report.
To realize these theoretical gains in practice, we designed and implemented H100 GPU kernels for the forward and backward that fuses the convolution operations with an online softmax in the style of Flash Attention. The kernel executes the entire attention operation in the compressed latent space of width E/C, which significantly reduces both the arithmetic intensity and data-movement requirements.
Our FLOP complexity model closely aligns with implementation results. The matrix multiplications of CCA reduce by a factor of 1/C. CCA’s lead grows with larger sequence lengths as the S² terms and projections dominate and the small overheads from convolutions, reductions, and kernel launch amortize. A key difference from methods that only rebalance bandwidth during decode (like GQA and MLA) is that CCA reduces both prefill and decode compute while simultaneously shrinking the KV-cache. CCGQA inherits GQA's KV reuse benefits in the latent while preserving CCA's 1/C scaling of the matrix multiplications. This enables CCA to provide significant performance benefits during training, prefill, and decode.
Our experimental ablations demonstrate that CCA and CCGQA consistently outperform both GQA and MLA at equal KV-cache compression on both dense and MoE models.
Dense Models: CCGQA outperforms all other attentions despite matching parameters—with substantial KV-cache compression compared to MHA. CCA beats MLA in the parameter-matched setting while using 4 times fewer FLOPs.
MoE Models: CCA achieves lower loss than GQA and MLA at equivalent parameter counts with less compute cost. CCGQA achieves 8× KV-cache compression, half the KV-cache of other parameter efficient attentions tested, with no drop in performance compared to standard MHA and other parameter efficient attentions such as MLA.
The full technical report, including ablation studies, kernel implementation details, and code examples, is available on arXiv. For an example of using CCA/CCGQA in a production model training run, see our ZAYA1 technical report.
Self-attention is the powerful sequence mixer at the core of modern transformer architectures, but its quadratic compute complexity and linearly-growing KV-cache create fundamental bottlenecks for training and serving large language models—especially at long context lengths. Prior works such as Grouped Query Attention (GQA) and Multi-Latent Attention (MLA) have made important strides in reducing the KV-cache size and reducing decode latency. However, these methods leave FLOPs—which determines prefill and training speed—either unchanged or even increased.
We introduce Compressed Convolutional Attention (CCA), a novel attention method which down-projects queries, keys, and values to lower-dimensional latent space and then, crucially, performs the entire attention operation inside the shared latent space, unlike other attention mechanisms such as GQA and MLA. Our design cuts parameters, KV-cache, and FLOPs all at once by the desired compression factor. Since CCA is orthogonal to head-sharing approaches, we can combine the two to form Compressed Convolutional Grouped Query Attention (CCGQA), which enables the model designer to tune compression toward either FLOP or memory limits without sacrificing model quality. CCGQA is used to power the ZAYA suite of language models.
CCA builds on the insight that significant redundancy exists in traditional attention's parameter and activation spaces. Rather than up-projecting compressed representations back to full dimension before attention (as in MLA), CCA performs the full attention computation entirely within the compressed latent space.
To maintain and enhance performance at high compression rates, CCA introduces three key innovations:
Convolutional Mixing: We apply sequential convolutions across both sequence and channel dimensions on the compressed query and key latents. These convolutions provide additional expressivity and enable better information transfer through attention—analogous to how causal convolutions improve sequence mixing in state-space models.
QK-Mean Adaptation: We add the mean of pre- and post-convolution query and key values, which shares information between Q and K while providing a skip connection that allows the model to interpolate convolution strength.
Value-Shift: Each attention head receives two distinct value types—one from the current embedding and one from the previous position in the sequence. This inductive bias, similar to token-shift approaches in RWKV, proves beneficial for sequence modeling.

CCA allows RoPE (or any position embedding) to be applied directly within the latent space. This is unlike competing latent methods like MLA, which requires a shared key rope head and cache due to its up-projections.
Furthermore, our work is the first to note and theoretically clarify that parameter-sharing methods (like GQA) and parameter-compression methods (like MLA and CCA) are orthogonal and can be effectively combined. CCGQA applies GQA-style K and V head sharing within the already compressed latent space. This enables an additional 2× KV-cache reduction without performance penalty, and allows decoupling the compression rates of queries and keys.
In addition, CCA and CCGQA are also amenable to existing parallelism schemes:
Tensor Parallelism: Sharding CCA's latent representation incurs only the same cost as GQA, as long as TP rank matches the number of kv heads. The TP communication for QK mean can be overlapped with the compute of the convolutions.
Context Parallelism: One can communicate the smaller latent width E/C instead of full width E within ring or tree attention schemes.
Because the S² terms in QKᵀ and Attn·V shrink by 1/C (where C is the compression factor), the speedups grow with sequence length. On H100 GPUs, our fused CCA kernel reduces prefill latency by approximately 1.7× at sequence length 16k relative to MHA, and accelerates backward passes by approximately 1.3×.
CCA with 16× compression enables √16 = 4× longer sequences to be processed for the same FLOP budget. For a full theoretical FLOP analysis of CCA against its competitors, see Table II and Figure 2 (below) of the technical report.
To realize these theoretical gains in practice, we designed and implemented H100 GPU kernels for the forward and backward that fuses the convolution operations with an online softmax in the style of Flash Attention. The kernel executes the entire attention operation in the compressed latent space of width E/C, which significantly reduces both the arithmetic intensity and data-movement requirements.
Our FLOP complexity model closely aligns with implementation results. The matrix multiplications of CCA reduce by a factor of 1/C. CCA’s lead grows with larger sequence lengths as the S² terms and projections dominate and the small overheads from convolutions, reductions, and kernel launch amortize. A key difference from methods that only rebalance bandwidth during decode (like GQA and MLA) is that CCA reduces both prefill and decode compute while simultaneously shrinking the KV-cache. CCGQA inherits GQA's KV reuse benefits in the latent while preserving CCA's 1/C scaling of the matrix multiplications. This enables CCA to provide significant performance benefits during training, prefill, and decode.

Our experimental ablations demonstrate that CCA and CCGQA consistently outperform both GQA and MLA at equal KV-cache compression on both dense and MoE models.
Dense Models: CCGQA outperforms all other attentions despite matching parameters—with substantial KV-cache compression compared to MHA. CCA beats MLA in the parameter-matched setting while using 4 times fewer FLOPs.
MoE Models: CCA achieves lower loss than GQA and MLA at equivalent parameter counts with less compute cost. CCGQA achieves 8× KV-cache compression, half the KV-cache of other parameter efficient attentions tested, with no drop in performance compared to standard MHA and other parameter efficient attentions such as MLA.

The full technical report, including ablation studies, kernel implementation details, and code examples, is available on arXiv. For an example of using CCA/CCGQA in a production model training run, see our ZAYA1 technical report.




Self-attention is the powerful sequence mixer at the core of modern transformer architectures, but its quadratic compute complexity and linearly-growing KV-cache create fundamental bottlenecks for training and serving large language models—especially at long context lengths. Prior works such as Grouped Query Attention (GQA) and Multi-Latent Attention (MLA) have made important strides in reducing the KV-cache size and reducing decode latency. However, these methods leave FLOPs—which determines prefill and training speed—either unchanged or even increased.
We introduce Compressed Convolutional Attention (CCA), a novel attention method which down-projects queries, keys, and values to lower-dimensional latent space and then, crucially, performs the entire attention operation inside the shared latent space, unlike other attention mechanisms such as GQA and MLA. Our design cuts parameters, KV-cache, and FLOPs all at once by the desired compression factor. Since CCA is orthogonal to head-sharing approaches, we can combine the two to form Compressed Convolutional Grouped Query Attention (CCGQA), which enables the model designer to tune compression toward either FLOP or memory limits without sacrificing model quality. CCGQA is used to power the ZAYA suite of language models.
CCA builds on the insight that significant redundancy exists in traditional attention's parameter and activation spaces. Rather than up-projecting compressed representations back to full dimension before attention (as in MLA), CCA performs the full attention computation entirely within the compressed latent space.
To maintain and enhance performance at high compression rates, CCA introduces three key innovations:
Convolutional Mixing: We apply sequential convolutions across both sequence and channel dimensions on the compressed query and key latents. These convolutions provide additional expressivity and enable better information transfer through attention—analogous to how causal convolutions improve sequence mixing in state-space models.
QK-Mean Adaptation: We add the mean of pre- and post-convolution query and key values, which shares information between Q and K while providing a skip connection that allows the model to interpolate convolution strength.
Value-Shift: Each attention head receives two distinct value types—one from the current embedding and one from the previous position in the sequence. This inductive bias, similar to token-shift approaches in RWKV, proves beneficial for sequence modeling.
CCA allows RoPE (or any position embedding) to be applied directly within the latent space. This is unlike competing latent methods like MLA, which requires a shared key rope head and cache due to its up-projections.
Furthermore, our work is the first to note and theoretically clarify that parameter-sharing methods (like GQA) and parameter-compression methods (like MLA and CCA) are orthogonal and can be effectively combined. CCGQA applies GQA-style K and V head sharing within the already compressed latent space. This enables an additional 2× KV-cache reduction without performance penalty, and allows decoupling the compression rates of queries and keys.
In addition, CCA and CCGQA are also amenable to existing parallelism schemes:
Tensor Parallelism: Sharding CCA's latent representation incurs only the same cost as GQA, as long as TP rank matches the number of kv heads. The TP communication for QK mean can be overlapped with the compute of the convolutions.
Context Parallelism: One can communicate the smaller latent width E/C instead of full width E within ring or tree attention schemes.

Because the S² terms in QKᵀ and Attn·V shrink by 1/C (where C is the compression factor), the speedups grow with sequence length. On H100 GPUs, our fused CCA kernel reduces prefill latency by approximately 1.7× at sequence length 16k relative to MHA, and accelerates backward passes by approximately 1.3×.
CCA with 16× compression enables √16 = 4× longer sequences to be processed for the same FLOP budget. For a full theoretical FLOP analysis of CCA against its competitors, see Table II and Figure 2 (below) of the technical report.

To realize these theoretical gains in practice, we designed and implemented H100 GPU kernels for the forward and backward that fuses the convolution operations with an online softmax in the style of Flash Attention. The kernel executes the entire attention operation in the compressed latent space of width E/C, which significantly reduces both the arithmetic intensity and data-movement requirements.
Our FLOP complexity model closely aligns with implementation results. The matrix multiplications of CCA reduce by a factor of 1/C. CCA’s lead grows with larger sequence lengths as the S² terms and projections dominate and the small overheads from convolutions, reductions, and kernel launch amortize. A key difference from methods that only rebalance bandwidth during decode (like GQA and MLA) is that CCA reduces both prefill and decode compute while simultaneously shrinking the KV-cache. CCGQA inherits GQA's KV reuse benefits in the latent while preserving CCA's 1/C scaling of the matrix multiplications. This enables CCA to provide significant performance benefits during training, prefill, and decode.
Our experimental ablations demonstrate that CCA and CCGQA consistently outperform both GQA and MLA at equal KV-cache compression on both dense and MoE models.
Dense Models: CCGQA outperforms all other attentions despite matching parameters—with substantial KV-cache compression compared to MHA. CCA beats MLA in the parameter-matched setting while using 4 times fewer FLOPs.
MoE Models: CCA achieves lower loss than GQA and MLA at equivalent parameter counts with less compute cost. CCGQA achieves 8× KV-cache compression, half the KV-cache of other parameter efficient attentions tested, with no drop in performance compared to standard MHA and other parameter efficient attentions such as MLA.
The full technical report, including ablation studies, kernel implementation details, and code examples, is available on arXiv. For an example of using CCA/CCGQA in a production model training run, see our ZAYA1 technical report.



Self-attention is the powerful sequence mixer at the core of modern transformer architectures, but its quadratic compute complexity and linearly-growing KV-cache create fundamental bottlenecks for training and serving large language models—especially at long context lengths. Prior works such as Grouped Query Attention (GQA) and Multi-Latent Attention (MLA) have made important strides in reducing the KV-cache size and reducing decode latency. However, these methods leave FLOPs—which determines prefill and training speed—either unchanged or even increased.
We introduce Compressed Convolutional Attention (CCA), a novel attention method which down-projects queries, keys, and values to lower-dimensional latent space and then, crucially, performs the entire attention operation inside the shared latent space, unlike other attention mechanisms such as GQA and MLA. Our design cuts parameters, KV-cache, and FLOPs all at once by the desired compression factor. Since CCA is orthogonal to head-sharing approaches, we can combine the two to form Compressed Convolutional Grouped Query Attention (CCGQA), which enables the model designer to tune compression toward either FLOP or memory limits without sacrificing model quality. CCGQA is used to power the ZAYA suite of language models.

CCA builds on the insight that significant redundancy exists in traditional attention's parameter and activation spaces. Rather than up-projecting compressed representations back to full dimension before attention (as in MLA), CCA performs the full attention computation entirely within the compressed latent space.
To maintain and enhance performance at high compression rates, CCA introduces three key innovations:
Convolutional Mixing: We apply sequential convolutions across both sequence and channel dimensions on the compressed query and key latents. These convolutions provide additional expressivity and enable better information transfer through attention—analogous to how causal convolutions improve sequence mixing in state-space models.
QK-Mean Adaptation: We add the mean of pre- and post-convolution query and key values, which shares information between Q and K while providing a skip connection that allows the model to interpolate convolution strength.
Value-Shift: Each attention head receives two distinct value types—one from the current embedding and one from the previous position in the sequence. This inductive bias, similar to token-shift approaches in RWKV, proves beneficial for sequence modeling.





CCA allows RoPE (or any position embedding) to be applied directly within the latent space. This is unlike competing latent methods like MLA, which requires a shared key rope head and cache due to its up-projections.
Furthermore, our work is the first to note and theoretically clarify that parameter-sharing methods (like GQA) and parameter-compression methods (like MLA and CCA) are orthogonal and can be effectively combined. CCGQA applies GQA-style K and V head sharing within the already compressed latent space. This enables an additional 2× KV-cache reduction without performance penalty, and allows decoupling the compression rates of queries and keys.
In addition, CCA and CCGQA are also amenable to existing parallelism schemes:
Tensor Parallelism: Sharding CCA's latent representation incurs only the same cost as GQA, as long as TP rank matches the number of kv heads. The TP communication for QK mean can be overlapped with the compute of the convolutions.
Context Parallelism: One can communicate the smaller latent width E/C instead of full width E within ring or tree attention schemes.
Self-attention is the powerful sequence mixer at the core of modern transformer architectures, but its quadratic compute complexity and linearly-growing KV-cache create fundamental bottlenecks for training and serving large language models—especially at long context lengths. Prior works such as Grouped Query Attention (GQA) and Multi-Latent Attention (MLA) have made important strides in reducing the KV-cache size and reducing decode latency. However, these methods leave FLOPs—which determines prefill and training speed—either unchanged or even increased.
We introduce Compressed Convolutional Attention (CCA), a novel attention method which down-projects queries, keys, and values to lower-dimensional latent space and then, crucially, performs the entire attention operation inside the shared latent space, unlike other attention mechanisms such as GQA and MLA. Our design cuts parameters, KV-cache, and FLOPs all at once by the desired compression factor. Since CCA is orthogonal to head-sharing approaches, we can combine the two to form Compressed Convolutional Grouped Query Attention (CCGQA), which enables the model designer to tune compression toward either FLOP or memory limits without sacrificing model quality. CCGQA is used to power the ZAYA suite of language models.

CCA builds on the insight that significant redundancy exists in traditional attention's parameter and activation spaces. Rather than up-projecting compressed representations back to full dimension before attention (as in MLA), CCA performs the full attention computation entirely within the compressed latent space.
To maintain and enhance performance at high compression rates, CCA introduces three key innovations:
Convolutional Mixing: We apply sequential convolutions across both sequence and channel dimensions on the compressed query and key latents. These convolutions provide additional expressivity and enable better information transfer through attention—analogous to how causal convolutions improve sequence mixing in state-space models.
QK-Mean Adaptation: We add the mean of pre- and post-convolution query and key values, which shares information between Q and K while providing a skip connection that allows the model to interpolate convolution strength.
Value-Shift: Each attention head receives two distinct value types—one from the current embedding and one from the previous position in the sequence. This inductive bias, similar to token-shift approaches in RWKV, proves beneficial for sequence modeling.
CCA allows RoPE (or any position embedding) to be applied directly within the latent space. This is unlike competing latent methods like MLA, which requires a shared key rope head and cache due to its up-projections.
Furthermore, our work is the first to note and theoretically clarify that parameter-sharing methods (like GQA) and parameter-compression methods (like MLA and CCA) are orthogonal and can be effectively combined. CCGQA applies GQA-style K and V head sharing within the already compressed latent space. This enables an additional 2× KV-cache reduction without performance penalty, and allows decoupling the compression rates of queries and keys.
In addition, CCA and CCGQA are also amenable to existing parallelism schemes:
Tensor Parallelism: Sharding CCA's latent representation incurs only the same cost as GQA, as long as TP rank matches the number of kv heads. The TP communication for QK mean can be overlapped with the compute of the convolutions.
Context Parallelism: One can communicate the smaller latent width E/C instead of full width E within ring or tree attention schemes.

Because the S² terms in QKᵀ and Attn·V shrink by 1/C (where C is the compression factor), the speedups grow with sequence length. On H100 GPUs, our fused CCA kernel reduces prefill latency by approximately 1.7× at sequence length 16k relative to MHA, and accelerates backward passes by approximately 1.3×.
CCA with 16× compression enables √16 = 4× longer sequences to be processed for the same FLOP budget. For a full theoretical FLOP analysis of CCA against its competitors, see Table II and Figure 2 (below) of the technical report.

To realize these theoretical gains in practice, we designed and implemented H100 GPU kernels for the forward and backward that fuses the convolution operations with an online softmax in the style of Flash Attention. The kernel executes the entire attention operation in the compressed latent space of width E/C, which significantly reduces both the arithmetic intensity and data-movement requirements.
Our FLOP complexity model closely aligns with implementation results. The matrix multiplications of CCA reduce by a factor of 1/C. CCA’s lead grows with larger sequence lengths as the S² terms and projections dominate and the small overheads from convolutions, reductions, and kernel launch amortize. A key difference from methods that only rebalance bandwidth during decode (like GQA and MLA) is that CCA reduces both prefill and decode compute while simultaneously shrinking the KV-cache. CCGQA inherits GQA's KV reuse benefits in the latent while preserving CCA's 1/C scaling of the matrix multiplications. This enables CCA to provide significant performance benefits during training, prefill, and decode.

Our experimental ablations demonstrate that CCA and CCGQA consistently outperform both GQA and MLA at equal KV-cache compression on both dense and MoE models.
Dense Models: CCGQA outperforms all other attentions despite matching parameters—with substantial KV-cache compression compared to MHA. CCA beats MLA in the parameter-matched setting while using 4 times fewer FLOPs.
MoE Models: CCA achieves lower loss than GQA and MLA at equivalent parameter counts with less compute cost. CCGQA achieves 8× KV-cache compression, half the KV-cache of other parameter efficient attentions tested, with no drop in performance compared to standard MHA and other parameter efficient attentions such as MLA.
The full technical report, including ablation studies, kernel implementation details, and code examples, is available on arXiv. For an example of using CCA/CCGQA in a production model training run, see our ZAYA1 technical report.

Self-attention is the powerful sequence mixer at the core of modern transformer architectures, but its quadratic compute complexity and linearly-growing KV-cache create fundamental bottlenecks for training and serving large language models—especially at long context lengths. Prior works such as Grouped Query Attention (GQA) and Multi-Latent Attention (MLA) have made important strides in reducing the KV-cache size and reducing decode latency. However, these methods leave FLOPs—which determines prefill and training speed—either unchanged or even increased.
We introduce Compressed Convolutional Attention (CCA), a novel attention method which down-projects queries, keys, and values to lower-dimensional latent space and then, crucially, performs the entire attention operation inside the shared latent space, unlike other attention mechanisms such as GQA and MLA. Our design cuts parameters, KV-cache, and FLOPs all at once by the desired compression factor. Since CCA is orthogonal to head-sharing approaches, we can combine the two to form Compressed Convolutional Grouped Query Attention (CCGQA), which enables the model designer to tune compression toward either FLOP or memory limits without sacrificing model quality. CCGQA is used to power the ZAYA suite of language models.
CCA builds on the insight that significant redundancy exists in traditional attention's parameter and activation spaces. Rather than up-projecting compressed representations back to full dimension before attention (as in MLA), CCA performs the full attention computation entirely within the compressed latent space.
To maintain and enhance performance at high compression rates, CCA introduces three key innovations:
Convolutional Mixing: We apply sequential convolutions across both sequence and channel dimensions on the compressed query and key latents. These convolutions provide additional expressivity and enable better information transfer through attention—analogous to how causal convolutions improve sequence mixing in state-space models.
QK-Mean Adaptation: We add the mean of pre- and post-convolution query and key values, which shares information between Q and K while providing a skip connection that allows the model to interpolate convolution strength.
Value-Shift: Each attention head receives two distinct value types—one from the current embedding and one from the previous position in the sequence. This inductive bias, similar to token-shift approaches in RWKV, proves beneficial for sequence modeling.
CCA allows RoPE (or any position embedding) to be applied directly within the latent space. This is unlike competing latent methods like MLA, which requires a shared key rope head and cache due to its up-projections.
Furthermore, our work is the first to note and theoretically clarify that parameter-sharing methods (like GQA) and parameter-compression methods (like MLA and CCA) are orthogonal and can be effectively combined. CCGQA applies GQA-style K and V head sharing within the already compressed latent space. This enables an additional 2× KV-cache reduction without performance penalty, and allows decoupling the compression rates of queries and keys.
In addition, CCA and CCGQA are also amenable to existing parallelism schemes:
Tensor Parallelism: Sharding CCA's latent representation incurs only the same cost as GQA, as long as TP rank matches the number of kv heads. The TP communication for QK mean can be overlapped with the compute of the convolutions.
Context Parallelism: One can communicate the smaller latent width E/C instead of full width E within ring or tree attention schemes.

To realize these theoretical gains in practice, we designed and implemented H100 GPU kernels for the forward and backward that fuses the convolution operations with an online softmax in the style of Flash Attention. The kernel executes the entire attention operation in the compressed latent space of width E/C, which significantly reduces both the arithmetic intensity and data-movement requirements.
Our FLOP complexity model closely aligns with implementation results. The matrix multiplications of CCA reduce by a factor of 1/C. CCA’s lead grows with larger sequence lengths as the S² terms and projections dominate and the small overheads from convolutions, reductions, and kernel launch amortize. A key difference from methods that only rebalance bandwidth during decode (like GQA and MLA) is that CCA reduces both prefill and decode compute while simultaneously shrinking the KV-cache. CCGQA inherits GQA's KV reuse benefits in the latent while preserving CCA's 1/C scaling of the matrix multiplications. This enables CCA to provide significant performance benefits during training, prefill, and decode.

Because the S² terms in QKᵀ and Attn·V shrink by 1/C (where C is the compression factor), the speedups grow with sequence length. On H100 GPUs, our fused CCA kernel reduces prefill latency by approximately 1.7× at sequence length 16k relative to MHA, and accelerates backward passes by approximately 1.3×.
CCA with 16× compression enables √16 = 4× longer sequences to be processed for the same FLOP budget. For a full theoretical FLOP analysis of CCA against its competitors, see Table II and Figure 2 (below) of the technical report.

Our experimental ablations demonstrate that CCA and CCGQA consistently outperform both GQA and MLA at equal KV-cache compression on both dense and MoE models.
Dense Models: CCGQA outperforms all other attentions despite matching parameters—with substantial KV-cache compression compared to MHA. CCA beats MLA in the parameter-matched setting while using 4 times fewer FLOPs.
MoE Models: CCA achieves lower loss than GQA and MLA at equivalent parameter counts with less compute cost. CCGQA achieves 8× KV-cache compression, half the KV-cache of other parameter efficient attentions tested, with no drop in performance compared to standard MHA and other parameter efficient attentions such as MLA.
The full technical report, including ablation studies, kernel implementation details, and code examples, is available on arXiv. For an example of using CCA/CCGQA in a production model training run, see our ZAYA1 technical report.
Self-attention is the powerful sequence mixer at the core of modern transformer architectures, but its quadratic compute complexity and linearly-growing KV-cache create fundamental bottlenecks for training and serving large language models—especially at long context lengths. Prior works such as Grouped Query Attention (GQA) and Multi-Latent Attention (MLA) have made important strides in reducing the KV-cache size and reducing decode latency. However, these methods leave FLOPs—which determines prefill and training speed—either unchanged or even increased.
We introduce Compressed Convolutional Attention (CCA), a novel attention method which down-projects queries, keys, and values to lower-dimensional latent space and then, crucially, performs the entire attention operation inside the shared latent space, unlike other attention mechanisms such as GQA and MLA. Our design cuts parameters, KV-cache, and FLOPs all at once by the desired compression factor. Since CCA is orthogonal to head-sharing approaches, we can combine the two to form Compressed Convolutional Grouped Query Attention (CCGQA), which enables the model designer to tune compression toward either FLOP or memory limits without sacrificing model quality. CCGQA is used to power the ZAYA suite of language models.
CCA builds on the insight that significant redundancy exists in traditional attention's parameter and activation spaces. Rather than up-projecting compressed representations back to full dimension before attention (as in MLA), CCA performs the full attention computation entirely within the compressed latent space.
To maintain and enhance performance at high compression rates, CCA introduces three key innovations:
Convolutional Mixing: We apply sequential convolutions across both sequence and channel dimensions on the compressed query and key latents. These convolutions provide additional expressivity and enable better information transfer through attention—analogous to how causal convolutions improve sequence mixing in state-space models.
QK-Mean Adaptation: We add the mean of pre- and post-convolution query and key values, which shares information between Q and K while providing a skip connection that allows the model to interpolate convolution strength.
Value-Shift: Each attention head receives two distinct value types—one from the current embedding and one from the previous position in the sequence. This inductive bias, similar to token-shift approaches in RWKV, proves beneficial for sequence modeling.


CCA allows RoPE (or any position embedding) to be applied directly within the latent space. This is unlike competing latent methods like MLA, which requires a shared key rope head and cache due to its up-projections.
Furthermore, our work is the first to note and theoretically clarify that parameter-sharing methods (like GQA) and parameter-compression methods (like MLA and CCA) are orthogonal and can be effectively combined. CCGQA applies GQA-style K and V head sharing within the already compressed latent space. This enables an additional 2× KV-cache reduction without performance penalty, and allows decoupling the compression rates of queries and keys.
In addition, CCA and CCGQA are also amenable to existing parallelism schemes:
Tensor Parallelism: Sharding CCA's latent representation incurs only the same cost as GQA, as long as TP rank matches the number of kv heads. The TP communication for QK mean can be overlapped with the compute of the convolutions.
Context Parallelism: One can communicate the smaller latent width E/C instead of full width E within ring or tree attention schemes.

Because the S² terms in QKᵀ and Attn·V shrink by 1/C (where C is the compression factor), the speedups grow with sequence length. On H100 GPUs, our fused CCA kernel reduces prefill latency by approximately 1.7× at sequence length 16k relative to MHA, and accelerates backward passes by approximately 1.3×.
CCA with 16× compression enables √16 = 4× longer sequences to be processed for the same FLOP budget. For a full theoretical FLOP analysis of CCA against its competitors, see Table II and Figure 2 (below) of the technical report.

To realize these theoretical gains in practice, we designed and implemented H100 GPU kernels for the forward and backward that fuses the convolution operations with an online softmax in the style of Flash Attention. The kernel executes the entire attention operation in the compressed latent space of width E/C, which significantly reduces both the arithmetic intensity and data-movement requirements.
Our FLOP complexity model closely aligns with implementation results. The matrix multiplications of CCA reduce by a factor of 1/C. CCA’s lead grows with larger sequence lengths as the S² terms and projections dominate and the small overheads from convolutions, reductions, and kernel launch amortize. A key difference from methods that only rebalance bandwidth during decode (like GQA and MLA) is that CCA reduces both prefill and decode compute while simultaneously shrinking the KV-cache. CCGQA inherits GQA's KV reuse benefits in the latent while preserving CCA's 1/C scaling of the matrix multiplications. This enables CCA to provide significant performance benefits during training, prefill, and decode.



Our experimental ablations demonstrate that CCA and CCGQA consistently outperform both GQA and MLA at equal KV-cache compression on both dense and MoE models.
Dense Models: CCGQA outperforms all other attentions despite matching parameters—with substantial KV-cache compression compared to MHA. CCA beats MLA in the parameter-matched setting while using 4 times fewer FLOPs.
MoE Models: CCA achieves lower loss than GQA and MLA at equivalent parameter counts with less compute cost. CCGQA achieves 8× KV-cache compression, half the KV-cache of other parameter efficient attentions tested, with no drop in performance compared to standard MHA and other parameter efficient attentions such as MLA.
The full technical report, including ablation studies, kernel implementation details, and code examples, is available on arXiv. For an example of using CCA/CCGQA in a production model training run, see our ZAYA1 technical report.
Self-attention is the powerful sequence mixer at the core of modern transformer architectures, but its quadratic compute complexity and linearly-growing KV-cache create fundamental bottlenecks for training and serving large language models—especially at long context lengths. Prior works such as Grouped Query Attention (GQA) and Multi-Latent Attention (MLA) have made important strides in reducing the KV-cache size and reducing decode latency. However, these methods leave FLOPs—which determines prefill and training speed—either unchanged or even increased.
We introduce Compressed Convolutional Attention (CCA), a novel attention method which down-projects queries, keys, and values to lower-dimensional latent space and then, crucially, performs the entire attention operation inside the shared latent space, unlike other attention mechanisms such as GQA and MLA. Our design cuts parameters, KV-cache, and FLOPs all at once by the desired compression factor. Since CCA is orthogonal to head-sharing approaches, we can combine the two to form Compressed Convolutional Grouped Query Attention (CCGQA), which enables the model designer to tune compression toward either FLOP or memory limits without sacrificing model quality. CCGQA is used to power the ZAYA suite of language models.
CCA builds on the insight that significant redundancy exists in traditional attention's parameter and activation spaces. Rather than up-projecting compressed representations back to full dimension before attention (as in MLA), CCA performs the full attention computation entirely within the compressed latent space.
To maintain and enhance performance at high compression rates, CCA introduces three key innovations:
Convolutional Mixing: We apply sequential convolutions across both sequence and channel dimensions on the compressed query and key latents. These convolutions provide additional expressivity and enable better information transfer through attention—analogous to how causal convolutions improve sequence mixing in state-space models.
QK-Mean Adaptation: We add the mean of pre- and post-convolution query and key values, which shares information between Q and K while providing a skip connection that allows the model to interpolate convolution strength.
Value-Shift: Each attention head receives two distinct value types—one from the current embedding and one from the previous position in the sequence. This inductive bias, similar to token-shift approaches in RWKV, proves beneficial for sequence modeling.
CCA allows RoPE (or any position embedding) to be applied directly within the latent space. This is unlike competing latent methods like MLA, which requires a shared key rope head and cache due to its up-projections.
Furthermore, our work is the first to note and theoretically clarify that parameter-sharing methods (like GQA) and parameter-compression methods (like MLA and CCA) are orthogonal and can be effectively combined. CCGQA applies GQA-style K and V head sharing within the already compressed latent space. This enables an additional 2× KV-cache reduction without performance penalty, and allows decoupling the compression rates of queries and keys.
In addition, CCA and CCGQA are also amenable to existing parallelism schemes:
Tensor Parallelism: Sharding CCA's latent representation incurs only the same cost as GQA, as long as TP rank matches the number of kv heads. The TP communication for QK mean can be overlapped with the compute of the convolutions.
Context Parallelism: One can communicate the smaller latent width E/C instead of full width E within ring or tree attention schemes.

Because the S² terms in QKᵀ and Attn·V shrink by 1/C (where C is the compression factor), the speedups grow with sequence length. On H100 GPUs, our fused CCA kernel reduces prefill latency by approximately 1.7× at sequence length 16k relative to MHA, and accelerates backward passes by approximately 1.3×.
CCA with 16× compression enables √16 = 4× longer sequences to be processed for the same FLOP budget. For a full theoretical FLOP analysis of CCA against its competitors, see Table II and Figure 2 (below) of the technical report.

To realize these theoretical gains in practice, we designed and implemented H100 GPU kernels for the forward and backward that fuses the convolution operations with an online softmax in the style of Flash Attention. The kernel executes the entire attention operation in the compressed latent space of width E/C, which significantly reduces both the arithmetic intensity and data-movement requirements.
Our FLOP complexity model closely aligns with implementation results. The matrix multiplications of CCA reduce by a factor of 1/C. CCA’s lead grows with larger sequence lengths as the S² terms and projections dominate and the small overheads from convolutions, reductions, and kernel launch amortize. A key difference from methods that only rebalance bandwidth during decode (like GQA and MLA) is that CCA reduces both prefill and decode compute while simultaneously shrinking the KV-cache. CCGQA inherits GQA's KV reuse benefits in the latent while preserving CCA's 1/C scaling of the matrix multiplications. This enables CCA to provide significant performance benefits during training, prefill, and decode.

Our experimental ablations demonstrate that CCA and CCGQA consistently outperform both GQA and MLA at equal KV-cache compression on both dense and MoE models.
Dense Models: CCGQA outperforms all other attentions despite matching parameters—with substantial KV-cache compression compared to MHA. CCA beats MLA in the parameter-matched setting while using 4 times fewer FLOPs.
MoE Models: CCA achieves lower loss than GQA and MLA at equivalent parameter counts with less compute cost. CCGQA achieves 8× KV-cache compression, half the KV-cache of other parameter efficient attentions tested, with no drop in performance compared to standard MHA and other parameter efficient attentions such as MLA.

The full technical report, including ablation studies, kernel implementation details, and code examples, is available on arXiv. For an example of using CCA/CCGQA in a production model training run, see our ZAYA1 technical report.





We present histograms depicting distribution of cluster sizes in all the datasets (see Fig. 7-11). Please, note that all the figures are in log-log scale. We see a significant drop in the number of clusters starting from the size of around 100. This drop is present both in DCLM and FineWeb-Edu2 (see Fig. 8 and 9 respectively), and most likely is explained by a combination of the deduplication strategy and quality when creating both datasets: DCLM deduplication was done individually within 10 shards, while FineWeb-Edu2 was deduplicated within every Common Crawl snapshot. We find that large clusters usually contain low quality material (repeated advertisements, license agreements templates, etc), so it’s not surprising that such documents were removed. Notably, DCLM still contained one cluster with the size close to 1 million documents, containing low quality documents seemingly coming from the advertisements (see Appendix).We find both Zyda-1and Dolma-CC contain a small amount of duplicates, which is expected, since both datasets were deduplicated globally by their authors. Remaining duplicates are likely false negatives from the initial deduplication procedure. Note, that distribution of duplicates clusters sizes of these two datasets (Fig. 10 and 11) don’t contain any sharp drops, but rather hyper exponentially decreases with cluster size.





Below is an example of the document from the largest cluster (~1M documents) of duplicates in DCLM (quality score 0.482627):
Is safe? Is scam?
Is safe for your PC?
Is safe or is it scam?
Domain is SafeSafe score: 1
The higher the number, the more dangerous the website.Any number higher than 1 means DANGER.
Positive votes:
Negative votes:
Vote Up Vote Down review
Have you had bad experience with Warn us, please!
Below one will find a few documents with different quality scores from DCLM coming from the same duplicates cluster. Quality score varies from ~0.2 to ~0.04.
Self-attention is the powerful sequence mixer at the core of modern transformer architectures, but its quadratic compute complexity and linearly-growing KV-cache create fundamental bottlenecks for training and serving large language models—especially at long context lengths. Prior works such as Grouped Query Attention (GQA) and Multi-Latent Attention (MLA) have made important strides in reducing the KV-cache size and reducing decode latency. However, these methods leave FLOPs—which determines prefill and training speed—either unchanged or even increased.
We introduce Compressed Convolutional Attention (CCA), a novel attention method which down-projects queries, keys, and values to lower-dimensional latent space and then, crucially, performs the entire attention operation inside the shared latent space, unlike other attention mechanisms such as GQA and MLA. Our design cuts parameters, KV-cache, and FLOPs all at once by the desired compression factor. Since CCA is orthogonal to head-sharing approaches, we can combine the two to form Compressed Convolutional Grouped Query Attention (CCGQA), which enables the model designer to tune compression toward either FLOP or memory limits without sacrificing model quality. CCGQA is used to power the ZAYA suite of language models.

Reported scores underlined.
Pass@1 scores with greedy sampling.
CCA builds on the insight that significant redundancy exists in traditional attention's parameter and activation spaces. Rather than up-projecting compressed representations back to full dimension before attention (as in MLA), CCA performs the full attention computation entirely within the compressed latent space.
To maintain and enhance performance at high compression rates, CCA introduces three key innovations:
Convolutional Mixing: We apply sequential convolutions across both sequence and channel dimensions on the compressed query and key latents. These convolutions provide additional expressivity and enable better information transfer through attention—analogous to how causal convolutions improve sequence mixing in state-space models.
QK-Mean Adaptation: We add the mean of pre- and post-convolution query and key values, which shares information between Q and K while providing a skip connection that allows the model to interpolate convolution strength.
Value-Shift: Each attention head receives two distinct value types—one from the current embedding and one from the previous position in the sequence. This inductive bias, similar to token-shift approaches in RWKV, proves beneficial for sequence modeling.


Pass@1 scores with greedy sampling. Livebench 2024-11-25.
Bold: Best score at 1.5B scale w/ greedy sampling
*reported scores
CCA allows RoPE (or any position embedding) to be applied directly within the latent space. This is unlike competing latent methods like MLA, which requires a shared key rope head and cache due to its up-projections.
Furthermore, our work is the first to note and theoretically clarify that parameter-sharing methods (like GQA) and parameter-compression methods (like MLA and CCA) are orthogonal and can be effectively combined. CCGQA applies GQA-style K and V head sharing within the already compressed latent space. This enables an additional 2× KV-cache reduction without performance penalty, and allows decoupling the compression rates of queries and keys.
In addition, CCA and CCGQA are also amenable to existing parallelism schemes:
Tensor Parallelism: Sharding CCA's latent representation incurs only the same cost as GQA, as long as TP rank matches the number of kv heads. The TP communication for QK mean can be overlapped with the compute of the convolutions.
Context Parallelism: One can communicate the smaller latent width E/C instead of full width E within ring or tree attention schemes.

Evals (reported underlined). All numbers pass@1 estimated using n=16
Because the S² terms in QKᵀ and Attn·V shrink by 1/C (where C is the compression factor), the speedups grow with sequence length. On H100 GPUs, our fused CCA kernel reduces prefill latency by approximately 1.7× at sequence length 16k relative to MHA, and accelerates backward passes by approximately 1.3×.
CCA with 16× compression enables √16 = 4× longer sequences to be processed for the same FLOP budget. For a full theoretical FLOP analysis of CCA against its competitors, see Table II and Figure 2 (below) of the technical report.

To realize these theoretical gains in practice, we designed and implemented H100 GPU kernels for the forward and backward that fuses the convolution operations with an online softmax in the style of Flash Attention. The kernel executes the entire attention operation in the compressed latent space of width E/C, which significantly reduces both the arithmetic intensity and data-movement requirements.
Our FLOP complexity model closely aligns with implementation results. The matrix multiplications of CCA reduce by a factor of 1/C. CCA’s lead grows with larger sequence lengths as the S² terms and projections dominate and the small overheads from convolutions, reductions, and kernel launch amortize. A key difference from methods that only rebalance bandwidth during decode (like GQA and MLA) is that CCA reduces both prefill and decode compute while simultaneously shrinking the KV-cache. CCGQA inherits GQA's KV reuse benefits in the latent while preserving CCA's 1/C scaling of the matrix multiplications. This enables CCA to provide significant performance benefits during training, prefill, and decode.

Our experimental ablations demonstrate that CCA and CCGQA consistently outperform both GQA and MLA at equal KV-cache compression on both dense and MoE models.
Dense Models: CCGQA outperforms all other attentions despite matching parameters—with substantial KV-cache compression compared to MHA. CCA beats MLA in the parameter-matched setting while using 4 times fewer FLOPs.
MoE Models: CCA achieves lower loss than GQA and MLA at equivalent parameter counts with less compute cost. CCGQA achieves 8× KV-cache compression, half the KV-cache of other parameter efficient attentions tested, with no drop in performance compared to standard MHA and other parameter efficient attentions such as MLA.
The full technical report, including ablation studies, kernel implementation details, and code examples, is available on arXiv. For an example of using CCA/CCGQA in a production model training run, see our ZAYA1 technical report.
Footnote: Training on the Eurus-2-RL dataset did not match the DeepScaleR math evaluation numbers, possibly due to lower quality synthetic math questions in NuminaMath-CoT providing a mixed training signal, or the solvability filtering process with QwQ-preview reducing the difficulty of the dataset. Additionally, the relatively small percentage of code (5%) likely led to math dominating training at the expense of code performance. Training on domain specific datasets and merging resulting models seems to be a potential way to counteract this problem, as demonstrated with SFT in Light-R1.
Self-attention is the powerful sequence mixer at the core of modern transformer architectures, but its quadratic compute complexity and linearly-growing KV-cache create fundamental bottlenecks for training and serving large language models—especially at long context lengths. Prior works such as Grouped Query Attention (GQA) and Multi-Latent Attention (MLA) have made important strides in reducing the KV-cache size and reducing decode latency. However, these methods leave FLOPs—which determines prefill and training speed—either unchanged or even increased.
We introduce Compressed Convolutional Attention (CCA), a novel attention method which down-projects queries, keys, and values to lower-dimensional latent space and then, crucially, performs the entire attention operation inside the shared latent space, unlike other attention mechanisms such as GQA and MLA. Our design cuts parameters, KV-cache, and FLOPs all at once by the desired compression factor. Since CCA is orthogonal to head-sharing approaches, we can combine the two to form Compressed Convolutional Grouped Query Attention (CCGQA), which enables the model designer to tune compression toward either FLOP or memory limits without sacrificing model quality. CCGQA is used to power the ZAYA suite of language models.

CCA builds on the insight that significant redundancy exists in traditional attention's parameter and activation spaces. Rather than up-projecting compressed representations back to full dimension before attention (as in MLA), CCA performs the full attention computation entirely within the compressed latent space.
To maintain and enhance performance at high compression rates, CCA introduces three key innovations:
Convolutional Mixing: We apply sequential convolutions across both sequence and channel dimensions on the compressed query and key latents. These convolutions provide additional expressivity and enable better information transfer through attention—analogous to how causal convolutions improve sequence mixing in state-space models.
QK-Mean Adaptation: We add the mean of pre- and post-convolution query and key values, which shares information between Q and K while providing a skip connection that allows the model to interpolate convolution strength.
Value-Shift: Each attention head receives two distinct value types—one from the current embedding and one from the previous position in the sequence. This inductive bias, similar to token-shift approaches in RWKV, proves beneficial for sequence modeling.
CCA allows RoPE (or any position embedding) to be applied directly within the latent space. This is unlike competing latent methods like MLA, which requires a shared key rope head and cache due to its up-projections.
Furthermore, our work is the first to note and theoretically clarify that parameter-sharing methods (like GQA) and parameter-compression methods (like MLA and CCA) are orthogonal and can be effectively combined. CCGQA applies GQA-style K and V head sharing within the already compressed latent space. This enables an additional 2× KV-cache reduction without performance penalty, and allows decoupling the compression rates of queries and keys.
In addition, CCA and CCGQA are also amenable to existing parallelism schemes:
Tensor Parallelism: Sharding CCA's latent representation incurs only the same cost as GQA, as long as TP rank matches the number of kv heads. The TP communication for QK mean can be overlapped with the compute of the convolutions.
Context Parallelism: One can communicate the smaller latent width E/C instead of full width E within ring or tree attention schemes.

Because the S² terms in QKᵀ and Attn·V shrink by 1/C (where C is the compression factor), the speedups grow with sequence length. On H100 GPUs, our fused CCA kernel reduces prefill latency by approximately 1.7× at sequence length 16k relative to MHA, and accelerates backward passes by approximately 1.3×.
CCA with 16× compression enables √16 = 4× longer sequences to be processed for the same FLOP budget. For a full theoretical FLOP analysis of CCA against its competitors, see Table II and Figure 2 (below) of the technical report.
To realize these theoretical gains in practice, we designed and implemented H100 GPU kernels for the forward and backward that fuses the convolution operations with an online softmax in the style of Flash Attention. The kernel executes the entire attention operation in the compressed latent space of width E/C, which significantly reduces both the arithmetic intensity and data-movement requirements.
Our FLOP complexity model closely aligns with implementation results. The matrix multiplications of CCA reduce by a factor of 1/C. CCA’s lead grows with larger sequence lengths as the S² terms and projections dominate and the small overheads from convolutions, reductions, and kernel launch amortize. A key difference from methods that only rebalance bandwidth during decode (like GQA and MLA) is that CCA reduces both prefill and decode compute while simultaneously shrinking the KV-cache. CCGQA inherits GQA's KV reuse benefits in the latent while preserving CCA's 1/C scaling of the matrix multiplications. This enables CCA to provide significant performance benefits during training, prefill, and decode.

Our experimental ablations demonstrate that CCA and CCGQA consistently outperform both GQA and MLA at equal KV-cache compression on both dense and MoE models.
Dense Models: CCGQA outperforms all other attentions despite matching parameters—with substantial KV-cache compression compared to MHA. CCA beats MLA in the parameter-matched setting while using 4 times fewer FLOPs.
MoE Models: CCA achieves lower loss than GQA and MLA at equivalent parameter counts with less compute cost. CCGQA achieves 8× KV-cache compression, half the KV-cache of other parameter efficient attentions tested, with no drop in performance compared to standard MHA and other parameter efficient attentions such as MLA.
The full technical report, including ablation studies, kernel implementation details, and code examples, is available on arXiv. For an example of using CCA/CCGQA in a production model training run, see our ZAYA1 technical report.
Self-attention is the powerful sequence mixer at the core of modern transformer architectures, but its quadratic compute complexity and linearly-growing KV-cache create fundamental bottlenecks for training and serving large language models—especially at long context lengths. Prior works such as Grouped Query Attention (GQA) and Multi-Latent Attention (MLA) have made important strides in reducing the KV-cache size and reducing decode latency. However, these methods leave FLOPs—which determines prefill and training speed—either unchanged or even increased.
We introduce Compressed Convolutional Attention (CCA), a novel attention method which down-projects queries, keys, and values to lower-dimensional latent space and then, crucially, performs the entire attention operation inside the shared latent space, unlike other attention mechanisms such as GQA and MLA. Our design cuts parameters, KV-cache, and FLOPs all at once by the desired compression factor. Since CCA is orthogonal to head-sharing approaches, we can combine the two to form Compressed Convolutional Grouped Query Attention (CCGQA), which enables the model designer to tune compression toward either FLOP or memory limits without sacrificing model quality. CCGQA is used to power the ZAYA suite of language models.
CCA builds on the insight that significant redundancy exists in traditional attention's parameter and activation spaces. Rather than up-projecting compressed representations back to full dimension before attention (as in MLA), CCA performs the full attention computation entirely within the compressed latent space.
To maintain and enhance performance at high compression rates, CCA introduces three key innovations:
Convolutional Mixing: We apply sequential convolutions across both sequence and channel dimensions on the compressed query and key latents. These convolutions provide additional expressivity and enable better information transfer through attention—analogous to how causal convolutions improve sequence mixing in state-space models.
QK-Mean Adaptation: We add the mean of pre- and post-convolution query and key values, which shares information between Q and K while providing a skip connection that allows the model to interpolate convolution strength.
Value-Shift: Each attention head receives two distinct value types—one from the current embedding and one from the previous position in the sequence. This inductive bias, similar to token-shift approaches in RWKV, proves beneficial for sequence modeling.

CCA allows RoPE (or any position embedding) to be applied directly within the latent space. This is unlike competing latent methods like MLA, which requires a shared key rope head and cache due to its up-projections.
Furthermore, our work is the first to note and theoretically clarify that parameter-sharing methods (like GQA) and parameter-compression methods (like MLA and CCA) are orthogonal and can be effectively combined. CCGQA applies GQA-style K and V head sharing within the already compressed latent space. This enables an additional 2× KV-cache reduction without performance penalty, and allows decoupling the compression rates of queries and keys.
In addition, CCA and CCGQA are also amenable to existing parallelism schemes:
Tensor Parallelism: Sharding CCA's latent representation incurs only the same cost as GQA, as long as TP rank matches the number of kv heads. The TP communication for QK mean can be overlapped with the compute of the convolutions.
Context Parallelism: One can communicate the smaller latent width E/C instead of full width E within ring or tree attention schemes.

Because the S² terms in QKᵀ and Attn·V shrink by 1/C (where C is the compression factor), the speedups grow with sequence length. On H100 GPUs, our fused CCA kernel reduces prefill latency by approximately 1.7× at sequence length 16k relative to MHA, and accelerates backward passes by approximately 1.3×.
CCA with 16× compression enables √16 = 4× longer sequences to be processed for the same FLOP budget. For a full theoretical FLOP analysis of CCA against its competitors, see Table II and Figure 2 (below) of the technical report.

To realize these theoretical gains in practice, we designed and implemented H100 GPU kernels for the forward and backward that fuses the convolution operations with an online softmax in the style of Flash Attention. The kernel executes the entire attention operation in the compressed latent space of width E/C, which significantly reduces both the arithmetic intensity and data-movement requirements.
Our FLOP complexity model closely aligns with implementation results. The matrix multiplications of CCA reduce by a factor of 1/C. CCA’s lead grows with larger sequence lengths as the S² terms and projections dominate and the small overheads from convolutions, reductions, and kernel launch amortize. A key difference from methods that only rebalance bandwidth during decode (like GQA and MLA) is that CCA reduces both prefill and decode compute while simultaneously shrinking the KV-cache. CCGQA inherits GQA's KV reuse benefits in the latent while preserving CCA's 1/C scaling of the matrix multiplications. This enables CCA to provide significant performance benefits during training, prefill, and decode.

Our experimental ablations demonstrate that CCA and CCGQA consistently outperform both GQA and MLA at equal KV-cache compression on both dense and MoE models.
Dense Models: CCGQA outperforms all other attentions despite matching parameters—with substantial KV-cache compression compared to MHA. CCA beats MLA in the parameter-matched setting while using 4 times fewer FLOPs.
MoE Models: CCA achieves lower loss than GQA and MLA at equivalent parameter counts with less compute cost. CCGQA achieves 8× KV-cache compression, half the KV-cache of other parameter efficient attentions tested, with no drop in performance compared to standard MHA and other parameter efficient attentions such as MLA.
The full technical report, including ablation studies, kernel implementation details, and code examples, is available on arXiv. For an example of using CCA/CCGQA in a production model training run, see our ZAYA1 technical report.
Self-attention is the powerful sequence mixer at the core of modern transformer architectures, but its quadratic compute complexity and linearly-growing KV-cache create fundamental bottlenecks for training and serving large language models—especially at long context lengths. Prior works such as Grouped Query Attention (GQA) and Multi-Latent Attention (MLA) have made important strides in reducing the KV-cache size and reducing decode latency. However, these methods leave FLOPs—which determines prefill and training speed—either unchanged or even increased.
We introduce Compressed Convolutional Attention (CCA), a novel attention method which down-projects queries, keys, and values to lower-dimensional latent space and then, crucially, performs the entire attention operation inside the shared latent space, unlike other attention mechanisms such as GQA and MLA. Our design cuts parameters, KV-cache, and FLOPs all at once by the desired compression factor. Since CCA is orthogonal to head-sharing approaches, we can combine the two to form Compressed Convolutional Grouped Query Attention (CCGQA), which enables the model designer to tune compression toward either FLOP or memory limits without sacrificing model quality. CCGQA is used to power the ZAYA suite of language models.
CCA builds on the insight that significant redundancy exists in traditional attention's parameter and activation spaces. Rather than up-projecting compressed representations back to full dimension before attention (as in MLA), CCA performs the full attention computation entirely within the compressed latent space.
To maintain and enhance performance at high compression rates, CCA introduces three key innovations:
Convolutional Mixing: We apply sequential convolutions across both sequence and channel dimensions on the compressed query and key latents. These convolutions provide additional expressivity and enable better information transfer through attention—analogous to how causal convolutions improve sequence mixing in state-space models.
QK-Mean Adaptation: We add the mean of pre- and post-convolution query and key values, which shares information between Q and K while providing a skip connection that allows the model to interpolate convolution strength.
Value-Shift: Each attention head receives two distinct value types—one from the current embedding and one from the previous position in the sequence. This inductive bias, similar to token-shift approaches in RWKV, proves beneficial for sequence modeling.
CCA allows RoPE (or any position embedding) to be applied directly within the latent space. This is unlike competing latent methods like MLA, which requires a shared key rope head and cache due to its up-projections.
Furthermore, our work is the first to note and theoretically clarify that parameter-sharing methods (like GQA) and parameter-compression methods (like MLA and CCA) are orthogonal and can be effectively combined. CCGQA applies GQA-style K and V head sharing within the already compressed latent space. This enables an additional 2× KV-cache reduction without performance penalty, and allows decoupling the compression rates of queries and keys.
In addition, CCA and CCGQA are also amenable to existing parallelism schemes:
Tensor Parallelism: Sharding CCA's latent representation incurs only the same cost as GQA, as long as TP rank matches the number of kv heads. The TP communication for QK mean can be overlapped with the compute of the convolutions.
Context Parallelism: One can communicate the smaller latent width E/C instead of full width E within ring or tree attention schemes.
Because the S² terms in QKᵀ and Attn·V shrink by 1/C (where C is the compression factor), the speedups grow with sequence length. On H100 GPUs, our fused CCA kernel reduces prefill latency by approximately 1.7× at sequence length 16k relative to MHA, and accelerates backward passes by approximately 1.3×.
CCA with 16× compression enables √16 = 4× longer sequences to be processed for the same FLOP budget. For a full theoretical FLOP analysis of CCA against its competitors, see Table II and Figure 2 (below) of the technical report.
To realize these theoretical gains in practice, we designed and implemented H100 GPU kernels for the forward and backward that fuses the convolution operations with an online softmax in the style of Flash Attention. The kernel executes the entire attention operation in the compressed latent space of width E/C, which significantly reduces both the arithmetic intensity and data-movement requirements.
Our FLOP complexity model closely aligns with implementation results. The matrix multiplications of CCA reduce by a factor of 1/C. CCA’s lead grows with larger sequence lengths as the S² terms and projections dominate and the small overheads from convolutions, reductions, and kernel launch amortize. A key difference from methods that only rebalance bandwidth during decode (like GQA and MLA) is that CCA reduces both prefill and decode compute while simultaneously shrinking the KV-cache. CCGQA inherits GQA's KV reuse benefits in the latent while preserving CCA's 1/C scaling of the matrix multiplications. This enables CCA to provide significant performance benefits during training, prefill, and decode.
Our experimental ablations demonstrate that CCA and CCGQA consistently outperform both GQA and MLA at equal KV-cache compression on both dense and MoE models.
Dense Models: CCGQA outperforms all other attentions despite matching parameters—with substantial KV-cache compression compared to MHA. CCA beats MLA in the parameter-matched setting while using 4 times fewer FLOPs.
MoE Models: CCA achieves lower loss than GQA and MLA at equivalent parameter counts with less compute cost. CCGQA achieves 8× KV-cache compression, half the KV-cache of other parameter efficient attentions tested, with no drop in performance compared to standard MHA and other parameter efficient attentions such as MLA.
Self-attention is the powerful sequence mixer at the core of modern transformer architectures, but its quadratic compute complexity and linearly-growing KV-cache create fundamental bottlenecks for training and serving large language models—especially at long context lengths. Prior works such as Grouped Query Attention (GQA) and Multi-Latent Attention (MLA) have made important strides in reducing the KV-cache size and reducing decode latency. However, these methods leave FLOPs—which determines prefill and training speed—either unchanged or even increased.
We introduce Compressed Convolutional Attention (CCA), a novel attention method which down-projects queries, keys, and values to lower-dimensional latent space and then, crucially, performs the entire attention operation inside the shared latent space, unlike other attention mechanisms such as GQA and MLA. Our design cuts parameters, KV-cache, and FLOPs all at once by the desired compression factor. Since CCA is orthogonal to head-sharing approaches, we can combine the two to form Compressed Convolutional Grouped Query Attention (CCGQA), which enables the model designer to tune compression toward either FLOP or memory limits without sacrificing model quality. CCGQA is used to power the ZAYA suite of language models.

CCA builds on the insight that significant redundancy exists in traditional attention's parameter and activation spaces. Rather than up-projecting compressed representations back to full dimension before attention (as in MLA), CCA performs the full attention computation entirely within the compressed latent space.
To maintain and enhance performance at high compression rates, CCA introduces three key innovations:
Convolutional Mixing: We apply sequential convolutions across both sequence and channel dimensions on the compressed query and key latents. These convolutions provide additional expressivity and enable better information transfer through attention—analogous to how causal convolutions improve sequence mixing in state-space models.
QK-Mean Adaptation: We add the mean of pre- and post-convolution query and key values, which shares information between Q and K while providing a skip connection that allows the model to interpolate convolution strength.
Value-Shift: Each attention head receives two distinct value types—one from the current embedding and one from the previous position in the sequence. This inductive bias, similar to token-shift approaches in RWKV, proves beneficial for sequence modeling.

CCA allows RoPE (or any position embedding) to be applied directly within the latent space. This is unlike competing latent methods like MLA, which requires a shared key rope head and cache due to its up-projections.
Furthermore, our work is the first to note and theoretically clarify that parameter-sharing methods (like GQA) and parameter-compression methods (like MLA and CCA) are orthogonal and can be effectively combined. CCGQA applies GQA-style K and V head sharing within the already compressed latent space. This enables an additional 2× KV-cache reduction without performance penalty, and allows decoupling the compression rates of queries and keys.
In addition, CCA and CCGQA are also amenable to existing parallelism schemes:
Tensor Parallelism: Sharding CCA's latent representation incurs only the same cost as GQA, as long as TP rank matches the number of kv heads. The TP communication for QK mean can be overlapped with the compute of the convolutions.
Context Parallelism: One can communicate the smaller latent width E/C instead of full width E within ring or tree attention schemes.
Because the S² terms in QKᵀ and Attn·V shrink by 1/C (where C is the compression factor), the speedups grow with sequence length. On H100 GPUs, our fused CCA kernel reduces prefill latency by approximately 1.7× at sequence length 16k relative to MHA, and accelerates backward passes by approximately 1.3×.
CCA with 16× compression enables √16 = 4× longer sequences to be processed for the same FLOP budget. For a full theoretical FLOP analysis of CCA against its competitors, see Table II and Figure 2 (below) of the technical report.

To realize these theoretical gains in practice, we designed and implemented H100 GPU kernels for the forward and backward that fuses the convolution operations with an online softmax in the style of Flash Attention. The kernel executes the entire attention operation in the compressed latent space of width E/C, which significantly reduces both the arithmetic intensity and data-movement requirements.
Our FLOP complexity model closely aligns with implementation results. The matrix multiplications of CCA reduce by a factor of 1/C. CCA’s lead grows with larger sequence lengths as the S² terms and projections dominate and the small overheads from convolutions, reductions, and kernel launch amortize. A key difference from methods that only rebalance bandwidth during decode (like GQA and MLA) is that CCA reduces both prefill and decode compute while simultaneously shrinking the KV-cache. CCGQA inherits GQA's KV reuse benefits in the latent while preserving CCA's 1/C scaling of the matrix multiplications. This enables CCA to provide significant performance benefits during training, prefill, and decode.

Our experimental ablations demonstrate that CCA and CCGQA consistently outperform both GQA and MLA at equal KV-cache compression on both dense and MoE models.
Dense Models: CCGQA outperforms all other attentions despite matching parameters—with substantial KV-cache compression compared to MHA. CCA beats MLA in the parameter-matched setting while using 4 times fewer FLOPs.
MoE Models: CCA achieves lower loss than GQA and MLA at equivalent parameter counts with less compute cost. CCGQA achieves 8× KV-cache compression, half the KV-cache of other parameter efficient attentions tested, with no drop in performance compared to standard MHA and other parameter efficient attentions such as MLA.

The full technical report, including ablation studies, kernel implementation details, and code examples, is available on arXiv. For an example of using CCA/CCGQA in a production model training run, see our ZAYA1 technical report.
Self-attention is the powerful sequence mixer at the core of modern transformer architectures, but its quadratic compute complexity and linearly-growing KV-cache create fundamental bottlenecks for training and serving large language models—especially at long context lengths. Prior works such as Grouped Query Attention (GQA) and Multi-Latent Attention (MLA) have made important strides in reducing the KV-cache size and reducing decode latency. However, these methods leave FLOPs—which determines prefill and training speed—either unchanged or even increased.
We introduce Compressed Convolutional Attention (CCA), a novel attention method which down-projects queries, keys, and values to lower-dimensional latent space and then, crucially, performs the entire attention operation inside the shared latent space, unlike other attention mechanisms such as GQA and MLA. Our design cuts parameters, KV-cache, and FLOPs all at once by the desired compression factor. Since CCA is orthogonal to head-sharing approaches, we can combine the two to form Compressed Convolutional Grouped Query Attention (CCGQA), which enables the model designer to tune compression toward either FLOP or memory limits without sacrificing model quality. CCGQA is used to power the ZAYA suite of language models.
CCA builds on the insight that significant redundancy exists in traditional attention's parameter and activation spaces. Rather than up-projecting compressed representations back to full dimension before attention (as in MLA), CCA performs the full attention computation entirely within the compressed latent space.
To maintain and enhance performance at high compression rates, CCA introduces three key innovations:
Convolutional Mixing: We apply sequential convolutions across both sequence and channel dimensions on the compressed query and key latents. These convolutions provide additional expressivity and enable better information transfer through attention—analogous to how causal convolutions improve sequence mixing in state-space models.
QK-Mean Adaptation: We add the mean of pre- and post-convolution query and key values, which shares information between Q and K while providing a skip connection that allows the model to interpolate convolution strength.
Value-Shift: Each attention head receives two distinct value types—one from the current embedding and one from the previous position in the sequence. This inductive bias, similar to token-shift approaches in RWKV, proves beneficial for sequence modeling.
CCA allows RoPE (or any position embedding) to be applied directly within the latent space. This is unlike competing latent methods like MLA, which requires a shared key rope head and cache due to its up-projections.
Furthermore, our work is the first to note and theoretically clarify that parameter-sharing methods (like GQA) and parameter-compression methods (like MLA and CCA) are orthogonal and can be effectively combined. CCGQA applies GQA-style K and V head sharing within the already compressed latent space. This enables an additional 2× KV-cache reduction without performance penalty, and allows decoupling the compression rates of queries and keys.
In addition, CCA and CCGQA are also amenable to existing parallelism schemes:
Tensor Parallelism: Sharding CCA's latent representation incurs only the same cost as GQA, as long as TP rank matches the number of kv heads. The TP communication for QK mean can be overlapped with the compute of the convolutions.
Context Parallelism: One can communicate the smaller latent width E/C instead of full width E within ring or tree attention schemes.
Because the S² terms in QKᵀ and Attn·V shrink by 1/C (where C is the compression factor), the speedups grow with sequence length. On H100 GPUs, our fused CCA kernel reduces prefill latency by approximately 1.7× at sequence length 16k relative to MHA, and accelerates backward passes by approximately 1.3×.
CCA with 16× compression enables √16 = 4× longer sequences to be processed for the same FLOP budget. For a full theoretical FLOP analysis of CCA against its competitors, see Table II and Figure 2 (below) of the technical report.
Self-attention is the powerful sequence mixer at the core of modern transformer architectures, but its quadratic compute complexity and linearly-growing KV-cache create fundamental bottlenecks for training and serving large language models—especially at long context lengths. Prior works such as Grouped Query Attention (GQA) and Multi-Latent Attention (MLA) have made important strides in reducing the KV-cache size and reducing decode latency. However, these methods leave FLOPs—which determines prefill and training speed—either unchanged or even increased.
We introduce Compressed Convolutional Attention (CCA), a novel attention method which down-projects queries, keys, and values to lower-dimensional latent space and then, crucially, performs the entire attention operation inside the shared latent space, unlike other attention mechanisms such as GQA and MLA. Our design cuts parameters, KV-cache, and FLOPs all at once by the desired compression factor. Since CCA is orthogonal to head-sharing approaches, we can combine the two to form Compressed Convolutional Grouped Query Attention (CCGQA), which enables the model designer to tune compression toward either FLOP or memory limits without sacrificing model quality. CCGQA is used to power the ZAYA suite of language models.
CCA builds on the insight that significant redundancy exists in traditional attention's parameter and activation spaces. Rather than up-projecting compressed representations back to full dimension before attention (as in MLA), CCA performs the full attention computation entirely within the compressed latent space.
To maintain and enhance performance at high compression rates, CCA introduces three key innovations:
Convolutional Mixing: We apply sequential convolutions across both sequence and channel dimensions on the compressed query and key latents. These convolutions provide additional expressivity and enable better information transfer through attention—analogous to how causal convolutions improve sequence mixing in state-space models.
QK-Mean Adaptation: We add the mean of pre- and post-convolution query and key values, which shares information between Q and K while providing a skip connection that allows the model to interpolate convolution strength.
Value-Shift: Each attention head receives two distinct value types—one from the current embedding and one from the previous position in the sequence. This inductive bias, similar to token-shift approaches in RWKV, proves beneficial for sequence modeling.
CCA allows RoPE (or any position embedding) to be applied directly within the latent space. This is unlike competing latent methods like MLA, which requires a shared key rope head and cache due to its up-projections.
Furthermore, our work is the first to note and theoretically clarify that parameter-sharing methods (like GQA) and parameter-compression methods (like MLA and CCA) are orthogonal and can be effectively combined. CCGQA applies GQA-style K and V head sharing within the already compressed latent space. This enables an additional 2× KV-cache reduction without performance penalty, and allows decoupling the compression rates of queries and keys.
In addition, CCA and CCGQA are also amenable to existing parallelism schemes:
Tensor Parallelism: Sharding CCA's latent representation incurs only the same cost as GQA, as long as TP rank matches the number of kv heads. The TP communication for QK mean can be overlapped with the compute of the convolutions.
Context Parallelism: One can communicate the smaller latent width E/C instead of full width E within ring or tree attention schemes.

Because the S² terms in QKᵀ and Attn·V shrink by 1/C (where C is the compression factor), the speedups grow with sequence length. On H100 GPUs, our fused CCA kernel reduces prefill latency by approximately 1.7× at sequence length 16k relative to MHA, and accelerates backward passes by approximately 1.3×.
CCA with 16× compression enables √16 = 4× longer sequences to be processed for the same FLOP budget. For a full theoretical FLOP analysis of CCA against its competitors, see Table II and Figure 2 (below) of the technical report.

To realize these theoretical gains in practice, we designed and implemented H100 GPU kernels for the forward and backward that fuses the convolution operations with an online softmax in the style of Flash Attention. The kernel executes the entire attention operation in the compressed latent space of width E/C, which significantly reduces both the arithmetic intensity and data-movement requirements.
Our FLOP complexity model closely aligns with implementation results. The matrix multiplications of CCA reduce by a factor of 1/C. CCA’s lead grows with larger sequence lengths as the S² terms and projections dominate and the small overheads from convolutions, reductions, and kernel launch amortize. A key difference from methods that only rebalance bandwidth during decode (like GQA and MLA) is that CCA reduces both prefill and decode compute while simultaneously shrinking the KV-cache. CCGQA inherits GQA's KV reuse benefits in the latent while preserving CCA's 1/C scaling of the matrix multiplications. This enables CCA to provide significant performance benefits during training, prefill, and decode.
Our experimental ablations demonstrate that CCA and CCGQA consistently outperform both GQA and MLA at equal KV-cache compression on both dense and MoE models.
Dense Models: CCGQA outperforms all other attentions despite matching parameters—with substantial KV-cache compression compared to MHA. CCA beats MLA in the parameter-matched setting while using 4 times fewer FLOPs.
MoE Models: CCA achieves lower loss than GQA and MLA at equivalent parameter counts with less compute cost. CCGQA achieves 8× KV-cache compression, half the KV-cache of other parameter efficient attentions tested, with no drop in performance compared to standard MHA and other parameter efficient attentions such as MLA.

The full technical report, including ablation studies, kernel implementation details, and code examples, is available on arXiv. For an example of using CCA/CCGQA in a production model training run, see our ZAYA1 technical report.


Self-attention is the powerful sequence mixer at the core of modern transformer architectures, but its quadratic compute complexity and linearly-growing KV-cache create fundamental bottlenecks for training and serving large language models—especially at long context lengths. Prior works such as Grouped Query Attention (GQA) and Multi-Latent Attention (MLA) have made important strides in reducing the KV-cache size and reducing decode latency. However, these methods leave FLOPs—which determines prefill and training speed—either unchanged or even increased.
We introduce Compressed Convolutional Attention (CCA), a novel attention method which down-projects queries, keys, and values to lower-dimensional latent space and then, crucially, performs the entire attention operation inside the shared latent space, unlike other attention mechanisms such as GQA and MLA. Our design cuts parameters, KV-cache, and FLOPs all at once by the desired compression factor. Since CCA is orthogonal to head-sharing approaches, we can combine the two to form Compressed Convolutional Grouped Query Attention (CCGQA), which enables the model designer to tune compression toward either FLOP or memory limits without sacrificing model quality. CCGQA is used to power the ZAYA suite of language models.

CCA builds on the insight that significant redundancy exists in traditional attention's parameter and activation spaces. Rather than up-projecting compressed representations back to full dimension before attention (as in MLA), CCA performs the full attention computation entirely within the compressed latent space.
To maintain and enhance performance at high compression rates, CCA introduces three key innovations:
Convolutional Mixing: We apply sequential convolutions across both sequence and channel dimensions on the compressed query and key latents. These convolutions provide additional expressivity and enable better information transfer through attention—analogous to how causal convolutions improve sequence mixing in state-space models.
QK-Mean Adaptation: We add the mean of pre- and post-convolution query and key values, which shares information between Q and K while providing a skip connection that allows the model to interpolate convolution strength.
Value-Shift: Each attention head receives two distinct value types—one from the current embedding and one from the previous position in the sequence. This inductive bias, similar to token-shift approaches in RWKV, proves beneficial for sequence modeling.

CCA allows RoPE (or any position embedding) to be applied directly within the latent space. This is unlike competing latent methods like MLA, which requires a shared key rope head and cache due to its up-projections.
Furthermore, our work is the first to note and theoretically clarify that parameter-sharing methods (like GQA) and parameter-compression methods (like MLA and CCA) are orthogonal and can be effectively combined. CCGQA applies GQA-style K and V head sharing within the already compressed latent space. This enables an additional 2× KV-cache reduction without performance penalty, and allows decoupling the compression rates of queries and keys.
In addition, CCA and CCGQA are also amenable to existing parallelism schemes:
Tensor Parallelism: Sharding CCA's latent representation incurs only the same cost as GQA, as long as TP rank matches the number of kv heads. The TP communication for QK mean can be overlapped with the compute of the convolutions.
Context Parallelism: One can communicate the smaller latent width E/C instead of full width E within ring or tree attention schemes.
Because the S² terms in QKᵀ and Attn·V shrink by 1/C (where C is the compression factor), the speedups grow with sequence length. On H100 GPUs, our fused CCA kernel reduces prefill latency by approximately 1.7× at sequence length 16k relative to MHA, and accelerates backward passes by approximately 1.3×.
CCA with 16× compression enables √16 = 4× longer sequences to be processed for the same FLOP budget. For a full theoretical FLOP analysis of CCA against its competitors, see Table II and Figure 2 (below) of the technical report.

To realize these theoretical gains in practice, we designed and implemented H100 GPU kernels for the forward and backward that fuses the convolution operations with an online softmax in the style of Flash Attention. The kernel executes the entire attention operation in the compressed latent space of width E/C, which significantly reduces both the arithmetic intensity and data-movement requirements.
Our FLOP complexity model closely aligns with implementation results. The matrix multiplications of CCA reduce by a factor of 1/C. CCA’s lead grows with larger sequence lengths as the S² terms and projections dominate and the small overheads from convolutions, reductions, and kernel launch amortize. A key difference from methods that only rebalance bandwidth during decode (like GQA and MLA) is that CCA reduces both prefill and decode compute while simultaneously shrinking the KV-cache. CCGQA inherits GQA's KV reuse benefits in the latent while preserving CCA's 1/C scaling of the matrix multiplications. This enables CCA to provide significant performance benefits during training, prefill, and decode.


Our experimental ablations demonstrate that CCA and CCGQA consistently outperform both GQA and MLA at equal KV-cache compression on both dense and MoE models.
Dense Models: CCGQA outperforms all other attentions despite matching parameters—with substantial KV-cache compression compared to MHA. CCA beats MLA in the parameter-matched setting while using 4 times fewer FLOPs.
MoE Models: CCA achieves lower loss than GQA and MLA at equivalent parameter counts with less compute cost. CCGQA achieves 8× KV-cache compression, half the KV-cache of other parameter efficient attentions tested, with no drop in performance compared to standard MHA and other parameter efficient attentions such as MLA.

The full technical report, including ablation studies, kernel implementation details, and code examples, is available on arXiv. For an example of using CCA/CCGQA in a production model training run, see our ZAYA1 technical report.
Self-attention is the powerful sequence mixer at the core of modern transformer architectures, but its quadratic compute complexity and linearly-growing KV-cache create fundamental bottlenecks for training and serving large language models—especially at long context lengths. Prior works such as Grouped Query Attention (GQA) and Multi-Latent Attention (MLA) have made important strides in reducing the KV-cache size and reducing decode latency. However, these methods leave FLOPs—which determines prefill and training speed—either unchanged or even increased.
We introduce Compressed Convolutional Attention (CCA), a novel attention method which down-projects queries, keys, and values to lower-dimensional latent space and then, crucially, performs the entire attention operation inside the shared latent space, unlike other attention mechanisms such as GQA and MLA. Our design cuts parameters, KV-cache, and FLOPs all at once by the desired compression factor. Since CCA is orthogonal to head-sharing approaches, we can combine the two to form Compressed Convolutional Grouped Query Attention (CCGQA), which enables the model designer to tune compression toward either FLOP or memory limits without sacrificing model quality. CCGQA is used to power the ZAYA suite of language models.

Self-attention is the powerful sequence mixer at the core of modern transformer architectures, but its quadratic compute complexity and linearly-growing KV-cache create fundamental bottlenecks for training and serving large language models—especially at long context lengths. Prior works such as Grouped Query Attention (GQA) and Multi-Latent Attention (MLA) have made important strides in reducing the KV-cache size and reducing decode latency. However, these methods leave FLOPs—which determines prefill and training speed—either unchanged or even increased.
We introduce Compressed Convolutional Attention (CCA), a novel attention method which down-projects queries, keys, and values to lower-dimensional latent space and then, crucially, performs the entire attention operation inside the shared latent space, unlike other attention mechanisms such as GQA and MLA. Our design cuts parameters, KV-cache, and FLOPs all at once by the desired compression factor. Since CCA is orthogonal to head-sharing approaches, we can combine the two to form Compressed Convolutional Grouped Query Attention (CCGQA), which enables the model designer to tune compression toward either FLOP or memory limits without sacrificing model quality. CCGQA is used to power the ZAYA suite of language models.

Self-attention is the powerful sequence mixer at the core of modern transformer architectures, but its quadratic compute complexity and linearly-growing KV-cache create fundamental bottlenecks for training and serving large language models—especially at long context lengths. Prior works such as Grouped Query Attention (GQA) and Multi-Latent Attention (MLA) have made important strides in reducing the KV-cache size and reducing decode latency. However, these methods leave FLOPs—which determines prefill and training speed—either unchanged or even increased.
We introduce Compressed Convolutional Attention (CCA), a novel attention method which down-projects queries, keys, and values to lower-dimensional latent space and then, crucially, performs the entire attention operation inside the shared latent space, unlike other attention mechanisms such as GQA and MLA. Our design cuts parameters, KV-cache, and FLOPs all at once by the desired compression factor. Since CCA is orthogonal to head-sharing approaches, we can combine the two to form Compressed Convolutional Grouped Query Attention (CCGQA), which enables the model designer to tune compression toward either FLOP or memory limits without sacrificing model quality. CCGQA is used to power the ZAYA suite of language models.

Self-attention is the powerful sequence mixer at the core of modern transformer architectures, but its quadratic compute complexity and linearly-growing KV-cache create fundamental bottlenecks for training and serving large language models—especially at long context lengths. Prior works such as Grouped Query Attention (GQA) and Multi-Latent Attention (MLA) have made important strides in reducing the KV-cache size and reducing decode latency. However, these methods leave FLOPs—which determines prefill and training speed—either unchanged or even increased.
We introduce Compressed Convolutional Attention (CCA), a novel attention method which down-projects queries, keys, and values to lower-dimensional latent space and then, crucially, performs the entire attention operation inside the shared latent space, unlike other attention mechanisms such as GQA and MLA. Our design cuts parameters, KV-cache, and FLOPs all at once by the desired compression factor. Since CCA is orthogonal to head-sharing approaches, we can combine the two to form Compressed Convolutional Grouped Query Attention (CCGQA), which enables the model designer to tune compression toward either FLOP or memory limits without sacrificing model quality. CCGQA is used to power the ZAYA suite of language models.

Self-attention is the powerful sequence mixer at the core of modern transformer architectures, but its quadratic compute complexity and linearly-growing KV-cache create fundamental bottlenecks for training and serving large language models—especially at long context lengths. Prior works such as Grouped Query Attention (GQA) and Multi-Latent Attention (MLA) have made important strides in reducing the KV-cache size and reducing decode latency. However, these methods leave FLOPs—which determines prefill and training speed—either unchanged or even increased.
We introduce Compressed Convolutional Attention (CCA), a novel attention method which down-projects queries, keys, and values to lower-dimensional latent space and then, crucially, performs the entire attention operation inside the shared latent space, unlike other attention mechanisms such as GQA and MLA. Our design cuts parameters, KV-cache, and FLOPs all at once by the desired compression factor. Since CCA is orthogonal to head-sharing approaches, we can combine the two to form Compressed Convolutional Grouped Query Attention (CCGQA), which enables the model designer to tune compression toward either FLOP or memory limits without sacrificing model quality. CCGQA is used to power the ZAYA suite of language models.

Self-attention is the powerful sequence mixer at the core of modern transformer architectures, but its quadratic compute complexity and linearly-growing KV-cache create fundamental bottlenecks for training and serving large language models—especially at long context lengths. Prior works such as Grouped Query Attention (GQA) and Multi-Latent Attention (MLA) have made important strides in reducing the KV-cache size and reducing decode latency. However, these methods leave FLOPs—which determines prefill and training speed—either unchanged or even increased.
We introduce Compressed Convolutional Attention (CCA), a novel attention method which down-projects queries, keys, and values to lower-dimensional latent space and then, crucially, performs the entire attention operation inside the shared latent space, unlike other attention mechanisms such as GQA and MLA. Our design cuts parameters, KV-cache, and FLOPs all at once by the desired compression factor. Since CCA is orthogonal to head-sharing approaches, we can combine the two to form Compressed Convolutional Grouped Query Attention (CCGQA), which enables the model designer to tune compression toward either FLOP or memory limits without sacrificing model quality. CCGQA is used to power the ZAYA suite of language models.

Self-attention is the powerful sequence mixer at the core of modern transformer architectures, but its quadratic compute complexity and linearly-growing KV-cache create fundamental bottlenecks for training and serving large language models—especially at long context lengths. Prior works such as Grouped Query Attention (GQA) and Multi-Latent Attention (MLA) have made important strides in reducing the KV-cache size and reducing decode latency. However, these methods leave FLOPs—which determines prefill and training speed—either unchanged or even increased.
We introduce Compressed Convolutional Attention (CCA), a novel attention method which down-projects queries, keys, and values to lower-dimensional latent space and then, crucially, performs the entire attention operation inside the shared latent space, unlike other attention mechanisms such as GQA and MLA. Our design cuts parameters, KV-cache, and FLOPs all at once by the desired compression factor. Since CCA is orthogonal to head-sharing approaches, we can combine the two to form Compressed Convolutional Grouped Query Attention (CCGQA), which enables the model designer to tune compression toward either FLOP or memory limits without sacrificing model quality. CCGQA is used to power the ZAYA suite of language models.

Self-attention is the powerful sequence mixer at the core of modern transformer architectures, but its quadratic compute complexity and linearly-growing KV-cache create fundamental bottlenecks for training and serving large language models—especially at long context lengths. Prior works such as Grouped Query Attention (GQA) and Multi-Latent Attention (MLA) have made important strides in reducing the KV-cache size and reducing decode latency. However, these methods leave FLOPs—which determines prefill and training speed—either unchanged or even increased.
We introduce Compressed Convolutional Attention (CCA), a novel attention method which down-projects queries, keys, and values to lower-dimensional latent space and then, crucially, performs the entire attention operation inside the shared latent space, unlike other attention mechanisms such as GQA and MLA. Our design cuts parameters, KV-cache, and FLOPs all at once by the desired compression factor. Since CCA is orthogonal to head-sharing approaches, we can combine the two to form Compressed Convolutional Grouped Query Attention (CCGQA), which enables the model designer to tune compression toward either FLOP or memory limits without sacrificing model quality. CCGQA is used to power the ZAYA suite of language models.
